EQUATIONS A DEUX INCONNUES DE TYPE ax+by+c=0⚓
Introduction
Les équations et systèmes d’équations à deux inconnue occupent une place importante en mathématiques. Ils sont utilisés pour traduire et résoudre une variété de problèmes de vie courante et dans différents domaines, tels que la géométrie, la physique et l'économie.
Vérifier qu'un couple est solution⚓
Méthode :
Pour vérifier qu’un couple \(( x_{0},y_{0})\) est solution ou non d’une équation à deux inconnues de type \(ax +by+c=0\)
je remplace x par \(x_{0}\) et y par \(y_{0}\) dans l’équation:
•Si l’égalité obtenue est vraie alors le couple\(( x_{0},y_{0})\)vérifie l’équation
Dans ce cas \(( x_{0},y_{0})\) est une solution de l’équation.
•Si l’égalité obtenue est fausse alors le couple \(( x_{0},y_{0})\)ne vérifie pas l’équation.Dans ce cas \(( x_{0},y_{0})\) n’est pas une solution de l’équation.
Exemple
Question⚓
On donne l’équation \(2x- 3y-1= 0\)
Vérifie si les couples \((2;1)\) et \((0;-3)\) sont solutions ou pas de cette équation.
Solution⚓
Vérification pour le couple \((2;1)\)
Je remplace \(x\) par \(2\) et \(y\) par dans l’équation
J’obtiens : \(2\times 2-3\times 1-1=0\)
c’est à dire \(4-3-1=0\)
ce qui donne \(4-4=0\)
Cette égalité est vraie donc le couple \((2;1)\) est solution de l’équation \(2x- 3y-1= 0\)
Vérification pour le couple \((0 ; -3)\)
Je remplace \(x\) par \(0\) et \(y\) par \(-3\) dans l’équation .
J’obtiens : \(2\times 0-3\times(-3)-1=0\)
c’est à dire \(3-1=0\)
Cette égalité est fausse donc le couple \((0 ; -3)\)n'est pas solution de l'équation \(2x- 3y-1= 0\)
Trouver un couple solution⚓
Méthode :
Pour trouver un couple solution d’une équation \(ax +by+c=\)à deux inconnues \(x\) et \(y\), je donne arbitrairement une valeur à l'une des inconnues
j'obtiens une équation à une seule inconnue que je résous pour trouver l'autre inconnue
Exemple :
On donne l'équation à deux inconnues suivante :
\(-4x- 3y +7= 0\)
Trouve un couple \((x,y)\) solution de cette équation
Solution
je peux donner à \(x\) la valeur \(1\)
J'obtiens: \(-4\times1-3y +7= 0\)
c'est à dire: \(-4-3y+7=0\)
ce qui donne \(-3y=-3\)
d'où \(y=1\)
Ainsi le couple \((-1;1)\) est une solution de l'équation : \(-4x- 3y +7= 0\)
Résoudre graphiquement une équation à deux inconnues⚓
Nota Bene :
On considère le plan muni d'un repère orthonormal
une équation de type \(ax+ by+c = 0\) où \(a\), \(b\) et \(c\) sont des nombres réels non tous nuls est une équation générale d'une droite.
Résoudre graphiquement cette équation revient à tracer dans le repère la droite d'équation \(ax+by+c=0\)
l'ensemble des couples de coordonnées des points de la droite représente l'ensemble des solutions de l'équation
Question⚓
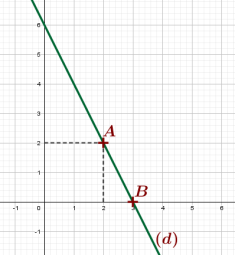
Résous graphiquement dans \(\mathbb{R}\times\mathbb{R}\) l'équation \(2x+y=6\)
Système d'équations à deux inconnues⚓
Résolution de systèmes d'équations à deux inconnues⚓
Méthode de substitution⚓
Méthode :
J’exprime l’une des inconnues en fonction de l’autre à l’aide de l’une des équations
Je remplace cette inconnue par son expression dans la deuxieme équation
Je résous l’équation à une inconnue obtenue pour trouver l’autre inconnue.
Question⚓
En utilisant la méthode de substitution, résous dans \(\mathbb{R}\times\mathbb{R}\)le système d'équations
\(\begin{cases}3x+y=9 ~~(i)\\2x-5y=-11 ~~(ii)\end{cases}\)
Solution⚓
Etape 1
J'exprime \(x\) à l'aide de \(y\) dans l'équation \((i)\)
\(y=9-3x\)
Etape 2
Je remplace y par cette expression dans l'équation \((ii)\) ce qui donne
\(2x-5(9-3x)=-11\)
c'est à dire \(2x-45+15x=-11\)
qui est équivalent \(17x=34\)
ce qui donne \(x=\dfrac{34}{17}\)
c'est à dire \(x=2\)
Etape 3
Je remplace \(x \)par\( 2\) dans l'équation \((ii)\)
et j'obtiens \(y=9-3\times{2}\)
Ce qui donne \(y=3\)
La solution du système d'équations est le couple \((2;3)\)
Méthode de combinaison ou d'élimination⚓
Méthode :
Je multiplie chacune des équations par un nombre bien choisi pour obtenir des coefficients opposés pour l’inconnue à éliminer
J’additionne membre à membre les deux équations pour éliminer une inconnue
Je calcule l’autre inconnue à l’aide de la relation obtenue;
Je peux reprendre l’opération pour l’autre inconnue
Question⚓
Résous dans \(\mathbb{R}\times\mathbb{R}\) en utilisant la méthode de combinaison le système d'équations suivant:
\(\begin{cases}3x+y=9\\2x-5y=-11\end{cases}\)
Solution⚓
\(\begin{cases}3x+y=9~~(I)\\2x-5y=-11 ~~(II)\end{cases}\)
J'élimine \(x\)
je multiplie les deux membres de la première équation par \(2\) et les deux membres de la deuxième équation par \(-3\)
Le système devient :
\(\begin{cases}3x+y=9\\2x-5y=11 \end{cases}\)
j'additionne membre à membre ces deux équations et j'obtiens :
\(4y=34\)
Ce qui donne \(x=7\)
Je reprends la même opération pour éliminer \(y\)
je multiplie les deux membres de la première équation par \(2\) et les deux membres de la deuxième équation par \(-3\)
Le système devient :
\(\begin{cases}3x+y=9\\2x-5y=11 \end{cases}\)
j'additionne membre à membre ces deux équations et j'obtiens :
\(4y=34\)
Ce qui donne \(x=7\)
La solution de l'équation est donc le couple \((3;7)\)
Question⚓
En utilisant la méthode de combinaison trouve l'ensemble des couples de nombres réels \((t ;z) \)solutions du système d'équations \(\begin{cases}2t+5z=1~~ (i)\\-3t+z=7~~ (ii)\end{cases}\)
Solution⚓
\(\begin{cases}2t+5z=1 ~~(i)\\-3t+z=7 ~~(ii)\end{cases}\)
J'élimine \(x\)
Je multiplie les deux membres de équation \((i)\) par \(3\) et les deux membres de l'équation \((ii)\) par \(2\)
Le système devient :
\(\begin{cases}6t+15z=3\\-6t+2z=14 \end{cases}\)
j'additionne membre à membre ces deux équations et j'obtiens :
\(17z=17\)
Ce qui donne \(z=1\)
\(\begin{cases}2t+5z=1~~ (i)\\-3t+z=7~~ (ii)\end{cases}\)
J'élimine \(x\)
Je multiplie les deux membres de l'équation \((ii)\) par \(-5\)
Le système devient :
\(\begin{cases}2t+5z=1~~ (i)\\15t-5z=-35~~ (ii)\end{cases}\)
j'additionne membre à membre ces deux équations et j'obtiens :
\(17t=-34\)
Ce qui donne \(t=-2\) La solution du système est le couple \((-2; 1)\)
Méthode d'égalité ou de comparaison⚓
Méthode :
J’exprime l’une des inconnues en fonction de l’autre dans les deux équations
J’obtiens une égalité qui est une équation à une inconnue
Je résous l’équation à une inconnue obtenue pour trouver l’une des inconnues
Je peux reprendre l’opération pour l’autre inconnue
Question⚓
Résous \(\mathbb{R}\times\mathbb{R}\)en utilisant la méthode de comparaison le système d'équations suivant :
\(\begin{cases}2f+5g=7\\4f+g=8\end{cases}\)
Les couple sont de la forme \((f;g)\)
Solution⚓
\(2f+5g=7\) est équivalent à \(g=\dfrac{7-3f}{2}\)
\(4f+g=8\) est équivalent à \(g=8-4f\)
Ces deux égalité permettent d'écrire \(\dfrac{7-3f}{2}=8-4f\) ce qui donne \(2(8-4f)=7-3f\) c'est à dire \(16-8f=7-3f\) d'où \(f=\dfrac{9}{5}\)
En remplaçant f par\(\dfrac{9}{5}\) on obtient \(g=\dfrac{4}{5}\).
La solution du système d'équation est le couple \((\dfrac{9}{5}; \dfrac{4}{5})\)
Méthode graphique⚓
Exemple :
Exemple
Je résous graphiquement le système d'équations à deux inconnues \(\begin{cases}-x+2y=4\\6x+y=-9\end{cases}\)
Je trace dans le même repère les droites \((d_{1}):x+2y=4\) et \((d_{2}):6x+y=-9\). Les droites se coupent en \(E(-2;3)\)
Le couple \((-2;3)\) est la solution du système.
Question⚓
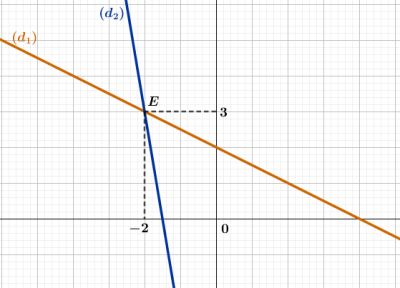
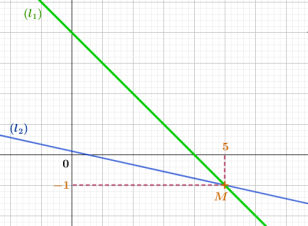
En utilisant la méthode graphique, résous dans \(\mathbb{R}\times\mathbb{R}\) le système d'équations suivant
\(\begin{cases}t+z=4\\2t+9z=1\end{cases}\)
Résolution de problèmes⚓
Méthode :
Les différentes étapes de la résolution de problème
Choix des inconnues
Mise en équations ou système d’équations
Résolution du système d’équations obtenue
Interprétation du résultat pour répondre à la question posée
Exemple :
Un théâtre propose deux types de billets les uns à \(1000F\) et les autres à \(2500F\). On sait que \(110\) spectateurs ont assisté à cette représentation théâtrale du samedi et que la recette totale s’élève à \(170000F\).
calcule le nombre de billets vendus pour chaque type.
SOLUTION
Choix des inconnues
\(n\) est le nombre de billets à \(1000F\) et \(m\) le nombre de billets à \(2500F\)
Mise en système d’équations
« \(110\) spectateurs ont assisté à cette représentation » :
se traduit par \(n+m=110\)
« la recette totale s’élève à \(170000F\) » se traduit par :
\(1000n+ 2500m=170000\)
J'obtiens ainsi le système
\(\begin{cases}n+m=110\\1000n+ 2500m=170000\end{cases}\)
Résolution du sytème
je resous ce sytème en utilisant l'une des méthodes vues et je trouve
\(n=70\) et \(m=40\)
Réponse à la question posée
\(70\) billets à \(1000\) \(F\) et \(40\) billets à \(2500\) \(F\) ont été vendus
Question⚓
Joël et Amadou ont en tout \(58\) timbres.La veille, Joël en avait deux fois plus que maintenant et Amadou en avait trois fois plus; s’ils les avaient réunis, ils en auraient \(143\) en tout.
Quel est le nombre de timbres que chacun d’eux a actuellement?
Solution⚓
Soient \(x\), le nombre de timbres de Joël et \(y\) le nombre de timbres d'Amadou
«Ils ont en tout \(58\) timbres» se trduit par : \(x+y=58\)
La veille, Joël en avait \(2x\) et Amadou en avait \(3y\)
«s’ils les avaient réunis, ils en auraient \(143\) en tout» se traduit par \(2x+3y=143\). J'obtiens ainsi le système de'équations suivant \(\begin{cases}x+y=58\\2x+3y=143\end{cases}\)
J'utilise l'une des méthode de resolution vues pour résoudre ce système et je trouve \(x=31\) et \(x=27\).
Joël a \(31\) timbres et Amadou en a \(27\).