Introduction
La notion de force est primitivement associée à l'idée d'un effort physique (musculaire). Cet effort permet de déplacer, de déformer, de mettre au repos, de briser....
D'autres causes permettent d'obtenir les mêmes effets.
Bien des systèmes (objets), soumis à deux forces, qui nous entourent sont immobiles (en équilibre) dans le référentiel terrestre. Existe-t-il alors une relation simple entre ces deux forces ?
Les actions mécaniques⚓
Qu'est-ce qu'une action mécanique?⚓
Définition :
Une action mécanique est toujours exercée par un objet (auteur) sur un autre objet (receveur).
Exemple :
Dans cet exemple de mise en mouvement du ballon, la chaussure est l'auteur de l'action mécanique et le ballon est le receveur.
Nota Bene : Effets
Une action mécanique se manifeste en réalité à partir de ses effets :
effet statique
équilibre (mise au repos)
déformation
effet dynamique
mise en mouvement
modification de la trajectoire
Les différentes actions mécaniques⚓
Il existe différents types d'action mécanique.
Les actions mécaniques de contact⚓
Il existe des actions mécaniques de contact qui nécessitent un contact entre l’auteur et le receveur.
Exemple : Tension d’un fil (localisée de contact)
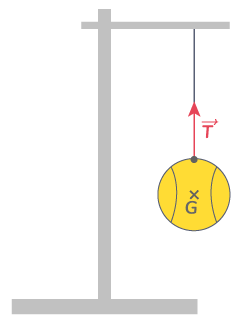
La tension d'un fil est une action mécanique de contact localisée au point d'attache fil-balle. Cette action empêche la boule de tomber.
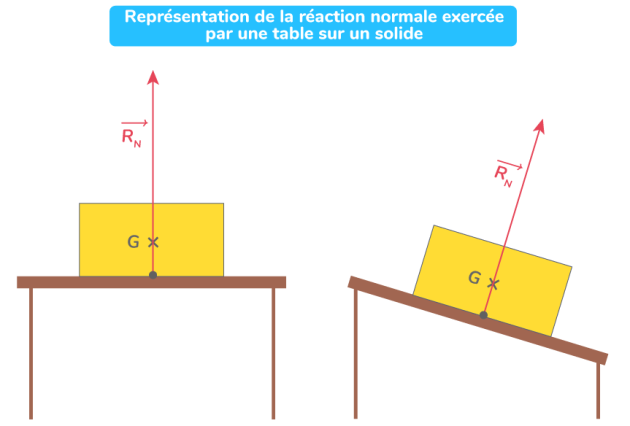
Exemple : Réaction du support (répartie de contact)
La réaction de la table sur la boite empêche la boite de s'enfoncer dans la table. C'est une action mécanique de contact et répartie.
Exemple : Action du vent sur une voile (répartie de contact)
Cette action mécanique de contact est répartie sur toute la voile car l'air agit sur toute la surface de la voile.
Nota Bene :
Les actions mécaniques peuvent être localisées : Le contact se fait sur une zone de faibles dimensions que l'on peut assimiler à un point (point d'application de l'action).
Les actions mécaniques peuvent aussi être réparties : le contact peut être réparti sur une surface importante.
Les actions mécaniques à distance⚓
Il existe également des actions mécaniques sans contact entre l’auteur et le receveur : on les appelle les actions mécaniques à distance.
Exemple : Action de pesanteur
Cette action mécanique agit sur les objets proches de la Terre. L'auteur est la Terre et le receveur est l'objet (la pomme) à proximité de la Terre. Cette action est notamment responsable de la chute des objets.
Exemple : Action magnétique
Si on approche une bille de fer d'un aimant, elle est attirée par l'aimant. La bille est le receveur de cette action mécanique et l'aimant est l'auteur.
Exemple : Action électrostatique
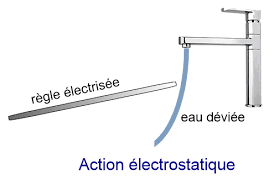
Si on approche une règle électrisée (que l'on a frotté vigoureusement avec un tissu) d'un mince filet d'eau, on observe que le filet d'eau est dévié. L'auteur de cette action est la règle et le receveur est l'eau.
vidéo
Nota Bene :
Les actions magnétique , électrostatique et de pesanteur sont des actions mécaniques à distance et réparties sur tout le volume du corps.
Applications⚓
La notion de force⚓
Définition⚓
Une force est toute cause capable ;
de mettre en mouvement ou de modifier le mouvement d'un corps
de déformer un corps.
Caractéristiques d’une force⚓
Une force est une action mécanique qui peut être modélisée par un vecteur.
Pour caractériser une force, il faut préciser :
son point d'application :
sa direction (droite d'action):
son sens :
son intensité :
Une force est une grandeur vectorielle.
Nota Bene :
L’intensité d’une force est mesurée à l’aide d’un dynamomètre.
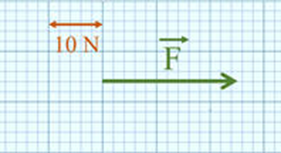
L'unité de la force est le Newton symbolisé par N.
Représentation vectorielle d’une force⚓
Une force se représente par un vecteur.
Exemple :
Un enfant tire un chariot à l’aide d’un fil. Le fil est attaché en un point A du chariot.
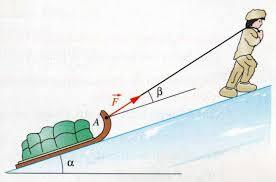
Le fil exerce une force localisée que nous pouvons représenter par le vecteur force (\(\vec{F}\)), dont on peut préciser ses caractéristiques :
son point d’application A (le point d’attache entre le fil et le chariot).
sa direction (celle du fil).
son sens (du chariot vers le fil).
son intensité (qui dépend de l’effort réalisé en N).
Exemple :
Exemple :
Applications⚓
Principe des actions réciproques ou principe de l’action et de la réaction.⚓
Enoncé :⚓
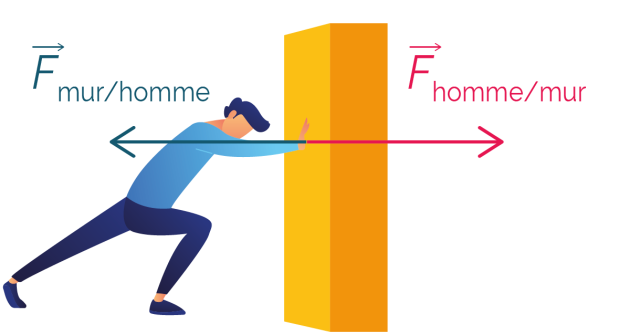
Lorsqu’un corps A exerce sur un corps B une force notée \(\vec{{F}_{A/B}}\), simultanément le corps B exerce sur A une force notée \(\vec{{F}_{B/A}}\) de même direction, de même intensité mais de sens contraire. La relation vectorielle traduisant cet énoncé est : \(\vec{{F}_{A/B}}\) = -\(\vec{{F}_{B/A}}\)
Exemple⚓
Applications⚓
Equilibre d'un solide soumis à deux forces⚓
Expérience⚓
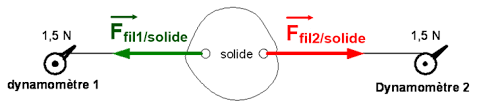
Le solide léger (de poids négligeable) est soumis à deux forces :
la force exercée par le fil 1 sur le solide
la force exercée par le fil 2 sur le solide
Le solide est en équilibre et on remarque que les deux forces ont même intensité (1,5 N), sont portées par la même droite d’action (les deux fils sont dans le prolongement l'un de l'autre), mais sont de sens opposés.
Conclusion⚓
Un corps, soumis à deux forces \(\vec{F}\) et \(\vec{F'}\), est en équilibre si les deux forces :
ont la même intensité
ont la même même direction (portées par le même support, c'est à dire des droites d'action confondues)
sont de sens opposés
Nota Bene :
Un corps, soumis à deux forces \(\vec{F}\) et \(\vec{F'}\), est en équilibre si les deux forces sont directement opposées (même intensité, même droite d'action (même support), sens contraires).
Ce qui se traduit par la relation vectorielle : \(\vec{F}\)=-\(\vec{F'}\) ou encore \(\vec{F}\) +\(\vec{F'}\)= \(\vec{0}\)