Introduction
Le chapitre sur la résistance électrique permet de consolider et d'approfondir les acquis des classes antérieures en électricité. La résistance électrique est utilisée en électrotechnique, en électronique...
Dans ce chapitre du programme en électricité tu vas découvrir la notion de résistance électrique d’un conducteur et établir la relation entre l’intensité du courant, la tension électrique et la résistance dans le cas d’un résistor. Cette relation traduit la loi d'ohm qui est une des lois fondamentales de l'électricité.
Les acquis tirés du chapitre peuvent te servir dans d'autres domaines :
ancrage interdisciplinaire (application concrète de la fonction linéaire (math)),
application dans la vie (gestion et prévision de phénomènes d’échauffement dans des appareils électriques usuels et circuits électroniques (technologie)).
A la fin de cette séquence, tu seras capable :
de donner l'énoncé de la loi d'ohm pour un résistor.
de déterminer expérimentalement la résistance d’un conducteur ohmique,
d'utiliser la loi d'Ohm,
d'expliquer et de prévenir certains phénomènes électriques.
Un résistor dans un circuit électrique⚓
Mise en évidence de la résistance
Visionne la vidéo ci-dessous et réponds aux questions suivantes :
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Après avoir comparé l’éclat de la lampe branchée seule à la pile avec l'éclat de la même lampe branchée à cette même pile en série avec le premier résistor, quelle est l’influence d’un résistor dans un circuit électrique en série?
Quelle est sa grandeur physique caractéristique ?
Quelle est l'unité légale de cette grandeur?
N.B: les réponses sont notées sur la partie réservée ci-dessous.
Conclusion
Lorsqu’un résistor est ajouté en série dans un circuit, l’intensité du courant diminue.
Les matériaux conducteurs électriques s’opposent plus ou moins au passage du courant électrique qui les traverse.
La grandeur physique qui caractérise cette opposition est appelée résistance électrique. Elle s’exprime en ohm (Ω).
Résistance d’un résistor : LOI D’OHM⚓
Méthode : Etude de la résistance d'un résistor
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
Complément :
Énoncé de la loi d’ohm : La tension U aux bornes d’un conducteur ohmique est égale au produit de la résistance R et l’intensité I du courant qui le traverse.
Expression de la loi d’ohm : U = RI ; I en ampères (A), U en volts (V) et R en ohms (Ω)
Nota Bene :
Le rhéostat permet de modifier simultanément l’intensité I du courant dans le circuit et la tension U aux bornes du résistor.
Complément : Détermination de la valeur d’une résistance
On peut déterminer la valeur d'une résistance par :
Mesures de U et de I puis utilisation de la relation R = \(\frac{U}{I}\) ;
Mesure directe avec un ohmmètre : un multimètre, utilisé en ohmmètre, permet de connaitre directement la valeur d’une résistance. Il suffit d'insérer le résistor entre les bornes de l'ohmmètre, le commutateur étant placé sur la position Ω comme l’indique la photo ci-contre.
Lecture des valeurs des résistances de certains dipôles utilisés dans les dispositifs électroniques avec le code des couleurs .
Contrôle des acquis
Complète les phrases suivantes.
Attention : clique sur la case et choisis le mot ou groupe de mots qui convient.
Exercice d'application 1
Question⚓
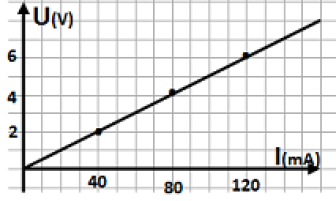
Pour déterminer expérimentalement la résistance d’un résistor, un élève de 3ème trace la courbe caractéristique U = f(I) donnée ci-contre.
liste le matériel nécessaire pour bien faire la manipulation.
Fais le schéma du montage
Déduis-en la valeur de la résistance R de ce résistor.
Détermine graphiquement l’intensité du courant qui le traverse lorsque la tension à ses bornes est égale à 4,5V.
Solution⚓
1) Liste du matériel nécessaire : Un générateur (pile), un ampèremètre, un voltmètre, des fils de connexion et un rhéostat.
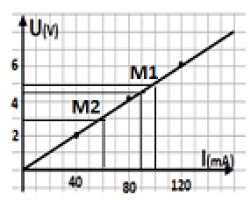
3) La valeur de la résistance R de ce résistor est : \(R=\frac{∆U}{∆I}=\ \frac{U(M_1)-U(M_2)}{I(M_1)-I(M_2)}\)= A.N : R = \(\frac{5-3}{0,1-0,06}\)= 50 Ω.
4) Graphiquement l’intensité I du courant qui traverse le résistor, lorsque la tension à ses bornes est égale à 4,5V, est de 90 mA
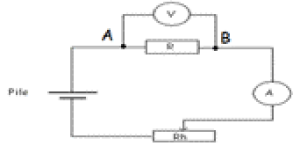
2) Schéma du montage
Exercice d'application 2
Question⚓
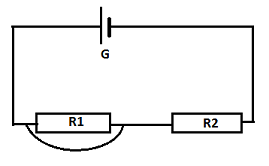
On réalise un circuit en série comprenant un générateur de tension constante U = 6 V et deux résistors de résistances respectives R1 et R2.
1) Détermine la tension U1 aux bornes du résistor de résistance R1 = 10 Ω, la tension U2 aux bornes du deuxième résistor et la valeur de sa résistance R2.
2) On branche un fil de résistance nulle aux bornes du résistor de résistance R1.
2.1) Détermine la nouvelle valeur de la tension U2 et la nouvelle valeur de l’intensité du courant qui traverse le circuit.
2.2) Quelle est la valeur de l’intensité du courant qui traverse alors le résistor de résistance R1. Justifie la réponse.
Solution⚓
1) Calcul des valeurs :
Calcul de la valeur de la tension U1:
Loi d’unicité et Loi d’ohm : I1 = I = 0,25 A et U1 = R1.I1 A.N: U1 = 10x0,25 = 2,5 V
Calcul de la valeur de la tension U2 :
Loi d'additivité des tensions : U = U1 + U2 → U2 = U - U1 A.N : U2 = 6 - 2,5 = 3,5 V
Calcul de la valeur de la résistance R2 :
Loi d’ohm : U2 = R2.I2 → \(R_2\ =\ \frac{U_2}{I_2}\) A.N: \(R_2\ =\ \frac{3,5}{0,,25}\) = 14 Ω
2.1) U = U2 et I = I2 car le résistor de résistance R1 est court-circuité.
U2 = R2.I2 → \(I_2\ =\ \frac{U}{R_2}\) A.N: \(I_2\ =\ \frac{6}{14}\) → I2 = 6/14 = 0,43 A
2.2) La valeur est nulle (I1 = 0 A) car le courant ne traverse pas ce résistor.
Association de résistors⚓
Définition : Résistance équivalente
La résistance équivalente à l’association de deux résistors de R1 et R2 est la résistance qui peut remplacer les résistances des deux résistors sans perturber l'état électrique du circuit électrique.
Complément : Association de résistors en série
La résistance équivalente à l’association de deux résistors de résistances respectives R1 et R2 en série est égale à la somme des résistances des deux résistors : Req = R1 + R2
Complément : Association de résistors en parallèle
Lorsqu’on associe en dérivation deux résistors de résistances respectives R1 et R2, alors l’inverse de la résistance équivalente Req du résistor équivalent est égal à la somme des inverses des résistances des deux résistors : \(\frac{1}{R_eq}\) = \(\frac{1}{R_1}\)+ \(\frac{1}{R_2}\)
Exercice d'application 1
Question⚓
Liste le matériel nécessaire aux montages pour déterminer par expérience la résistance équivalente à deux résistors de résistances respectives R1 = 6 Ω et R2 = 3 Ω montés en série puis en dérivation.
Calcule dans chacun des cas la valeur de la résistance équivalente.
Solution⚓
1) Liste du matériel : Un générateur, trois ampèremètres, trois voltmètres et des fils de connexion.
2) calcul des résistances équivalentes.
En série : Req = R1 + R2 A.N : Req = 6 + 3 = 9 Ω
En dérivation : \(\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2}\) → \(R_{eq} = \ \frac{R_1.R_2}{R_1 + \ R_2}\) A.N : \(R_{eq} = \frac{6 x 3}{6 + 3}\) = 2 Ω
Exercice d'application 2
Question⚓
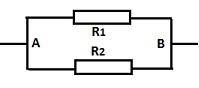
Un résistor de résistances R1 = 16 Ω est branché en dérivation avec un autre résistor de résistance R2= 12 Ω entre deux points A et B d’un circuit électrique. Le courant qui traverse le résistor de résistance R1 a pour intensité I1 = 3 A.
Détermine la résistance équivalente à ces deux résistors.
Calcule l’intensité du courant qui traverse le résistor de résistance R2.
Solution⚓
1) La résistance équivalente à ces deux résistors :
\(\frac{1}{R_{eq}} = \frac{1}{R_1}+\frac{1}{R_2}\) → \(R_{eq} = \ \frac{R_1R_2}{R_1+\ R_2}\) A.N : \(R_{eq} = \frac{16\ x12}{16+12}\) = 6,86 Ω
2) Calcule l’intensité du courant qui traverse le résistor de résistance R2 :
U1 = U2 → R1. I1 = R2. I2 → \(I_2 = \frac{R_1\ I_1}{R_2}\) A.N : \(I_2 = \frac{16x3}{12}\) = 4 A
Exercice d'application 3
Question⚓
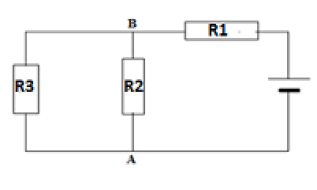
On réalise avec trois résistors de résistances R1, R2 et R3 le montage schématisé ci-contre. La résistance R du résistor équivalent à l’association des deux résistors en parallèle est égale à 2,4 Ω et la tension U aux bornes du générateur est de 24 V.
Sachant que R1 = 5,6 Ω, calcule la valeur de la résistance Req du résistor équivalent à l’association des trois résistors et l’intensité I du courant électrique débité par le générateur.
Quelle est la valeur de la tension aux bornes de chacun des résistors.
Quelle est la valeur de l’intensité du courant traversant chacun des résistors montés en dérivation sachant que R2 = 6 Ω? En déduire la valeur de R3.
Résistance d’un fil cylindrique homogène⚓
Nota Bene : Les facteurs qui influencent la résistance d’un fil cylindrique homogène
La résistance électrique d’un fil métallique homogène et cylindrique dépend de la nature et des caractéristiques géométriques (longueur et section) du fil.
Influence de la longueur du fil : la résistance d’un fil homogène cylindrique est proportionnelle à sa longueur.
Influence de la section du fil : la résistance d’un fil homogène cylindrique est proportionnelle à l’inverse de sa section.
Influence de la nature du fil : la résistance d’un fil homogène cylindrique dépend de la nature du fil. Chaque matériau est caractérisé par une grandeur physique appelée résistivité électrique et notée \(\rho\). Cette grandeur s’exprime en ohm.mètre (Ω.m). La résistance d’un fil est proportionnelle à sa résistivité.
Complément : Expression de la résistance
La résistance d’un fil homogène de section constante s, de longueur \(\ell\) et de résistivité \(\rho\) est donnée par la relation : \(R=\rho\frac{\ell}{S}\), R s’exprime en Ω, \(\rho\) en Ω.m, \(\ell\) en m et s en m2.
Exercice d'application 1
Question⚓
Sachant que la résistance du fil inséré dans un fer à repasser est R = 27,5 Ω, sa résistivité est ρ = 1,2.10-6 Ω.m et sa section est s = 0,6.10-6 m2, calcule la longueur du fil.
Exercice d'application 2
Exercice d'application 3
Question⚓
Un conducteur ohmique est constitué d’un fil cylindrique de cuivre de longueur \(\ell\) = 5 m dont la section a un rayon r = 37.10-6 m
Quelle est la valeur de la résistance R du conducteur ohmique ainsi constitué sachant que la résistivité électrique du cuivre est \(\rho\) = 1,6. 10-8 \(\Omega\).m.
Quelle est la valeur de la résistance R1 d’un autre fil de même section et de même nature que le précédent mais de longueur double ?