INTRODUCTION⚓
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
DEFINITION ET NOTATION D'UNE APPLICATION AFFINE⚓
Définition :
Soient \(a\) et \(b\) deux réels donnés. L'application affine \(f\) de coefficient \(a\) et de terme constant \(b\), est la correspondance qui à chaque réel \(x\) associe le nombre \(ax\) + \(b\). On écrit : \(f(x)\) = \(ax\) + \(b\).
\(f(x)\) est appelé l'image de \(x\) par l'application \(f\) et \(x\) est l'antécédent de \(f(x)\).
On peut aussi noter : \(f(x) = y = ax + b\) ; ainsi, \(y\) est appelé l'image de \(x\) par l'application \(f\) et \(x\) est l'antécédent de \(y\).
Exemple :
\(f(x)\) = \(-7x\) + \(13\), \(f\) est une application affine de coefficient \(-7\) et de terme constant \(13\).
\(g(x)\) = \(2x\), \(g\) est une application affine de coefficient \(2\) et de terme constant \(0\).
\(h(x)\) = \(-\sqrt{5}\), \(h\) est une application affine de coefficient \(0\) et de terme constant \(-\sqrt{5}\).
\(i(x) = 2x^2\), \(i\) n'est pas une application affine.
Exercice d'application
CALCULS D'IMAGES ET D'ANTECEDENTS D'UNE APPLICATION AFFINE⚓
Exemple :
Soit \(k\) une application affine définie par \(k(x)=3x-5,2\).
\(1)\) Calcule l'image de \(-2,4\) par l'application \(k\).
\(2\) Détermine l'antécédent de \(-3\) par l'application \(k\).
Solution
\(1)\) Dans \(k(x)=3x-5,2\), on remplace \(x\) par \(-2,4\).
\(k(-2,4)=3(-2,4)-5,2=-12,4\)
\(-12,4\) est l'image de \(-2,4\) par l'application \(k\).
\(2)\) On cherche \(x\) tel que \(k(x)=-3\) et on résout l'équation :
\(3x-5,2=-3\)
\(3x=2,2\)
\(x=\dfrac{2,2}{3}=\dfrac{11}{15}\)
\(\dfrac{11}{15}\) est l'antécédent de \(-3\) par l'application \(k\).
Question⚓
On considère une application affine g définie par \(g(x)=-\sqrt{3}x+5\).
\(1)\) Calcule les images de \(0\) et de \(\sqrt{3}\) par l'application \(g\).
\(2)\) Détermine les antécédents de \(-7\) et de \(5\) par l'application \(g\).
REPRESENTATION GRAPHIQUE D'UNE APPLICATION AFFINE⚓
Définition :
Soit l'application affine définie par \(f(x)\) = \(px\) + \(q\). Sa représentation graphique est la droite \(\left( \Delta \right)\) d'équation \(y\) = \(px\) + \(q\). Le réel \(p\) est appelé coefficient de la droite et \(b\) est l'ordonnée à l'origine.
Remarque
La droite \(\left( \Delta \right)\) d'équation \(y\) = \(px\) + \(q\) coupe l'axe des ordonnées en un point dont l'ordonnée est \(q\).
Méthode :
Le plan étant rapporté à un repère orthonormé \((O ;I ;J)\). Pour tracer la droite \(\left( \Delta \right)\), représentation graphique l'application affine \(f\) définie par \(f(x)\) = \(px\) + \(q\) :
on choisit deux nombres et on calcule leurs images. Chaque nombre et son image sont les coordonnées d'un point de la droite \(\left( \Delta \right)\) ;
on obtient ainsi deux points de la droite \(\left( \Delta \right)\) que l'on place dans le repère \((O ;I ;J)\) ;
on trace la droite qui passe par ces deux points qui est la droite \(\left( \Delta \right)\).
Exemple :
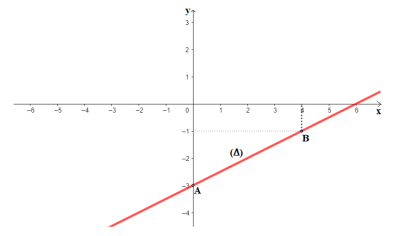
Dans le plan muni d’un repère \((O, I, J)\), trace la droite \(\left( \Delta \right)\), représentation graphique de l’application affine \(𝑓 \)définie par : \(𝑓(𝑥) = 0,5𝑥 − 3\).
Solution
On choisit deux nombres, par exemple : \(0\) et \(4\). On calcule les images de de ces deux nombres par l'application affine \(𝑓\). On résume les résultats dans le tableau ci-dessous :
\(x\) | \(0\) | \(4\) |
\(f(x)\) | \(-3\) | \(-1\) |
\(Point\) | \(A(0 ;-3)\) | \(B(4 ;-1)\) |
La représentation graphique de \(𝑓\) est la droite \(\left( \Delta \right) \)passant par les points \(𝐴\) et \(𝐵\).
Exercice d'application
DETERMINATION DE L'EXPRESSION LITTERALE D'UNE APPLICATION AFFINE⚓
Méthode :
Pour déterminer l'expression littérale \(f(x)\) = \(px\) + \(q\) de l'application affine \(f\), on cherche les valeurs de \(p\) et \(q\).
Exemple :
Premier cas : Détermine l'application affine \(g\) définie par \(g(5) = -9\) et de coefficient \(-2\).
Posons \(g(x)\) = \(px\) + \(q\), d'après les données \(g(x)\) = \(-2x\) + \(q\) et \(g(5)\) = \(-10\) + \(q\) \(= -9\) donc \(q = 1\) d'où \(g(x)\) = \(-2x\) + \(1\).
Deuxième cas : Détermine l'application affine \(h\) définie par \(h(1) = -1\) et \(h(-2) = -7\).
Posons \(h(x)\) = \(px\) + \(q\), d'après les données \(h(1)\) = \(p\) + \(q\) \(= -1\) et \(h(-2)\) = \(-2p\) + \(q\) \(= -7\). On obtient un système d'équations à deux inconnues dont la résolution donne \(p = 2\) et \(q = -3\). L'application affine est : \(h(x)\) = \(2x\) - \(3\).
Complément : Ci-dessous la version vidéo de l'exemple précédent.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.
APPLICATION AFFINE PAR INTERVALLE DU TYPE : f(x) = |mx + p|⚓
Méthode :
Pour représenter graphiquement une application affine du type \(f\left( x\right) =\left| mx+p\right|\) :
on exprime \(f(x)\) sans le symbole de la valeur absolue dans l'intervalle \(] -\infty ;-\dfrac{p}{m}]\), puis dans un repère orthonormal \((O, I, J)\) on représente \(f\) en se limitant à cet intervalle ;
on exprime \(f(x)\) sans le symbole de la valeur absolue dans l'intervalle \([ -\dfrac{p}{m};+\infty [\), puis dans le même repère, on représente \(f\) en se limitant à cet intervalle.
Exemple :
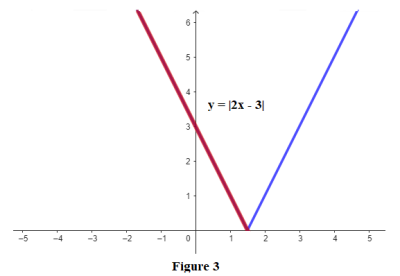
Représente dans un repère orthonormal l'application \(f\) définie par : \(k\left( x\right) =\left| 2x-3\right|\).
Dans \(]-\infty ;\frac{3}{2}]\), \(k(x) = -2x + 3\). Sa représentation graphique est la demi-droite de couleur rouge.
Dans \([ \dfrac{3}{2};+\infty [\), \(k(x) = 2x - 3\). Sa représentation graphique est la demi-droite de couleur bleue.
Les deux demi-droites (rouge et bleue) forment la représentation graphique de l'application \(f\) définie par : \(k\left( x\right) =\left| 2x-3\right|\).
JE TESTE MES CONNAISSANCES⚓
Question⚓
Monsieur Ndiaye doit effectuer avec sa voiture un voyage à Kédougou pour prendre part à la cérémonie d’ouverture d’un nouveau collège. A la fin de cette cérémonie, il doit retourner à Dakar. Les deux villes sont distantes de \(800\) \(km\).
On sait que la quantité \(q\) (en litres) d’essence restante dans la voiture après une distance parcourue \(x\) (en kilomètres), est une application affine et qu’après \(100\) \(km\) du trajet la consommation d’essence est d’environ \(5\) litres.
Avant le départ à Dakar, Monsieur Ndiaye a rempli son réservoir dont la capacité est de \(60\) litres d’essence.
Il dit à son fils élève en classe de troisième, qu’avant de tomber en panne sèche (le réservoir vide), le voyant lumineux devrait s’allumer lorsqu’il reste seulement \(5\) litres d’essence dans le réservoir. Mais ce voyant a un défaut et ne fonctionne pas.
Afin de prendre toutes les dispositions pour éviter la panne sèche, Monsieur Ndiaye voudrait savoir la distance à parcourir de Kédougou au lieu où le voyant lumineux devrait s’allumer. Il ne sait pas comment procéder. Son fils veut lui apporter son aide.
\(1)\) Détermine la quantité d’essence restante après un parcours de \(100\) \(Km\).
\(2)\) Démontre que la quantité \(q\) d’essence restante est telle que : \(q(x)\) = \(-\dfrac{1}{20}x+60\).
\(3)\) \(a)\) Détermine la distance parcourue après laquelle le voyant lumineux devrait s’allumer.
\(3)\) \(b)\) Déduis-en la distance à parcourir de Kédougou au lieu où le voyant devrait s’allumer.