• contenu
  • menu
  • pied de page

TRANSFORMATIONS DU PLAN

Titre de l'activité : TRANSFORMATIONS DU PLAN
Résumé

A la fin de ce chapitre, vous devez être capables de reconnaître la transformation résultant de deux translations successives, de deux symétries centrales successives et de deux symétries orthogonales successives.

Cycle : 3 : CM1, CM2, 6ème
Auteur(s) : 
  • ABOUBACAR SOUMANO
    Lycée Mame Yelli Badiane / IREMPT/ FST IA Pikine Guédiawaye
Licence : Creative Commons - Attribution - Partage dans les Mêmes Conditions

INTRODUCTION⚓

Impossible d'accéder à la ressource audio ou vidéo à l'adresse :

La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger le média.

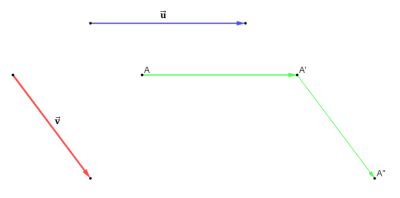
ETUDE DE DEUX TRANSLATIONS SUCCESSIVES⚓

Activité⚓

Consigne

Observe la figure ci-contre.

Complète les propositions ci-dessous, puis ordonne les pour découvrir la définition de deux translations successives.

\(1)\) \(t_{\overrightarrow{u}}\left( A\right) =A'\) signifie \(\overrightarrow{A...}=\overrightarrow{u}\)

\(2)\) \(t_{\overrightarrow{v}}\left( A'\right) =...\) signifie \(\overrightarrow{A'...}=\overrightarrow{v}\)

\(3)\) \(\overrightarrow{AA''}=\overrightarrow{AA'}+\overrightarrow{A'A''}=\) \(\overrightarrow{u}+{...}\)

\(4)\) \(\overrightarrow{AA''}=\overrightarrow{u}+{...}\) signifie \(t_\left( \overrightarrow{u}+\overrightarrow{v}\right) \left( A\right) =\) \(A''\)

\(\overrightarrow{AA''}=\overrightarrow{AA'}+\overrightarrow{A'A''}=\) \(\overrightarrow{u}+\overrightarrow{v}\)

\(\overrightarrow{AA''}=\overrightarrow{u}+\overrightarrow{v}\) signifie \(t_\left( \overrightarrow{u}+\overrightarrow{v}\right) \left( A\right) =\) \(A''\)

\(t_{\overrightarrow{v}}\left( A'\right) =A''\) signifie \(\overrightarrow{A'A''}=\overrightarrow{v}\)

\(t_{\overrightarrow{u}}\left( A\right) =A'\) signifie \(\overrightarrow{AA'}=\overrightarrow{u}\)

Plus d'éléments à ordonner
Déposez ici
CorrectionRecommencer

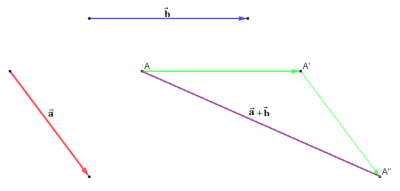
Propriété⚓

Soient \(\overrightarrow{a}\) et \(\overrightarrow{b}\) deux vecteurs distincts. Faire la translation de vecteur \(\overrightarrow{a}\) suivie de la translation de vecteur \(\overrightarrow{b}\) revient à faire la translation de vecteur \(\overrightarrow{a}\) \(+\) \(\overrightarrow{b}\).

Exercice d'application⚓

Question⚓

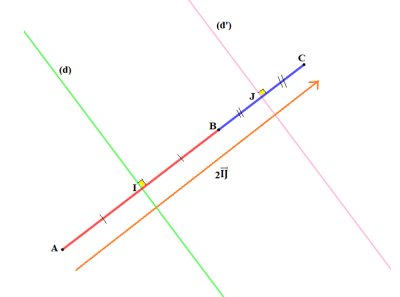
Soient \(\overrightarrow{a}\) et \(\overrightarrow{b}\) deux vecterus de même direction tel que \(\overrightarrow{b}=3\overrightarrow{a}\). Soit \(M\) un point du plan.

\(1)\) Construit l'image \(M''\) de \(M\) par la translation de vecteur \(\overrightarrow{a}\) suiuvie de la translation de vecteur \(\overrightarrow{b}\).

\(2)\) Montre que \(\overrightarrow{MM''}\) et \(\overrightarrow{a}\) sont colinéaires.

ETUDE DE DEUX SYMETRIES CENTRALES SUCCESSIVES⚓

Activité⚓

Consigne

Observe la figure ci-contre.

Complète les propositions ci-dessous, puis ordonne les pour découvrir la définition de deux symétries centrales successives.

\(\overrightarrow{IK}=\overrightarrow{...}+\overrightarrow{JK}\)

\(\overrightarrow{IJ}=...\overrightarrow{OJ}\) et \(\overrightarrow{JK}=...\overrightarrow{JO'}\)

\(\overrightarrow{IK}=\overrightarrow{...}+\overrightarrow{...}\) \(=2\overrightarrow{00}'\)

\(\overrightarrow{IJ}=2\overrightarrow{OJ}\) et \(\overrightarrow{JK}=2\overrightarrow{JO'}\)

\(\overrightarrow{IK}=\overrightarrow{IJ}+\overrightarrow{JK}\)

\(\overrightarrow{IK}=2\overrightarrow{OJ}+2\overrightarrow{JO'}\) \(=2\overrightarrow{00}'\)

Plus d'éléments à ordonner
Déposez ici
CorrectionRecommencer

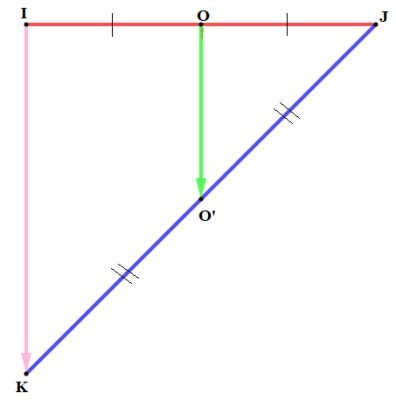
Propriété⚓

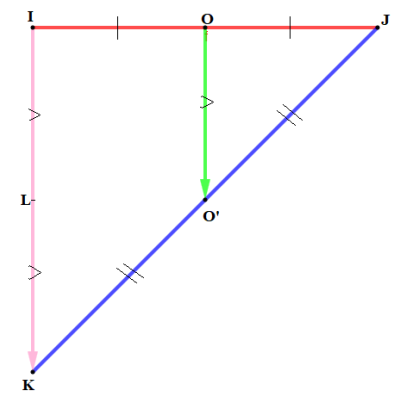
Soient \(O\) et \(O'\) deux oints distincts du plan. Faire une symétrie centrale de centre \(O\) suivie d'une symétrie centrale de centre \(O'\) revient à faire la translation de vecteur \(2\overrightarrow{00}'\).

Exercice d'application⚓

Question⚓

Soit \(RTS\) un triangle.

\(1)\) Construis le point \(R'\) image du point \(R\) par la symétrie de centre \(T\).

\(2)\) Construis le point \(R''\) image du point \(R'\) par la symétrie de centre \(S\).

\(3)\) Montre que \(\overrightarrow{RR''}\) \(=\) \(2\overrightarrow{TS}\) sont colinéaires.

ETUDE DE DEUX SYMETIRIES ORTHOGONALES SUCCESSIVES⚓

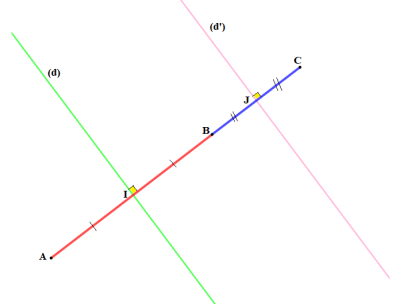
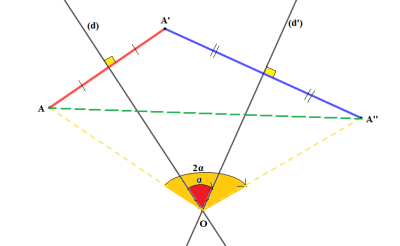
Les deux droites sont strictement parallèles⚓

Activité⚓

Consigne

Observe la figure ci-contre.

Complète en remplaçant les pointillés par la lettre qui convient dans les propositions ci-dessous, puis ordonne les pour découvrir la définition de deux symétries orthogonales successives où \((d)\) et \((d')\) sont parallèles.

\(\overrightarrow{AB}=2\overrightarrow{...B}\)

\(\overrightarrow{BC}=2\overrightarrow{B...}\)

\(\overrightarrow{AC}=2\overrightarrow{...B}+2\overrightarrow{B...}=2\overrightarrow{...}\)

\(B\) et \(C\) sont symétriques par rapport \(J\) donc \(\overrightarrow{BC}=2\overrightarrow{BJ}\)

\(A\) et \(B\) sont symétriques par rapport \(I\) donc \(\overrightarrow{AB}=2\overrightarrow{IB}\) et

Alors \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}=2\overrightarrow{IB}+2\overrightarrow{BJ}=2\overrightarrow{IJ}\)

Plus d'éléments à ordonner
Déposez ici
CorrectionRecommencer

propriété⚓

Soient \((d)\) et \((d')\) deux droites parallèles. Faire la symétrie orthogonale d'axe (d) suivie de la symétrie orthogonale d'axe (d'), revient à faire une translation de vecteur \(2\overrightarrow{IJ}\). \(IJ\) étant la distance entre les deux droites \((d)\) et \((d')\).

Les deux droites sont perpendiculaires⚓

Propriété

Soient \((d)\) et \((d')\) deux droites perpendiculaires en un point \(O\). Faire la symétrie orthogonale d'axe \((d)\) suivie de la symétrie orthogonale d'axe \((d')\), revient à faire la symétrie centrale de centre \(O\).

Les deux droites sont sécantes en un point I⚓

Propriété

Soient \((d)\) et \((d')\) deux droites perpendiculaires en un point \(O\) et formant un angle \(\alpha\). Faire la symétrie orthogonale d'axe \((d)\) suivie de la symétrie orthogonale d'axe \((d')\), revient à faire la rotation de centre \(O\) et d'angle de mesure \(2\alpha\).

Exercice d'application⚓

Question⚓

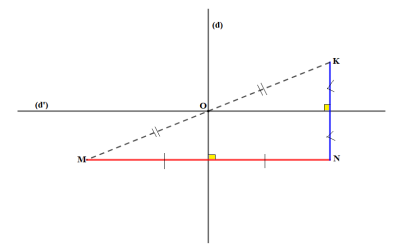
\(1)\) Place un point \(K\) dans le plan.

\(2)\) Trace deux droites \((d)\) et \((d')\) sécantes en \(O\) et formant un angle de \(65^o\).

\(3)\) Construis le point \(K'\) image de \(K\) par la symétrie d'axe \((d)\) puis onstruis le point \(K''\) image de \(K'\) par la symétrie d'axe \((d')\). Que représente \(K''\) pour \(K\) ?

JE TESTE MES CONNAISSANCES⚓

  • INTRODUCTION
  • ETUDE DE DEUX TRANSLATIONS SUCCESSIVES
    • Activité
      • Consigne
    • Propriété
    • Exercice d'application
      • Question⚓
  • ETUDE DE DEUX SYMETRIES CENTRALES SUCCESSIVES
    • Activité
      • Consigne
    • Propriété
    • Exercice d'application
      • Question⚓
  • ETUDE DE DEUX SYMETIRIES ORTHOGONALES SUCCESSIVES
    • Les deux droites sont strictement parallèles
      • Activité
        • Consigne
      • propriété
    • Les deux droites sont perpendiculaires
      • Les deux droites sont sécantes en un point I
        • Exercice d'application
          • Question⚓
      Réalisé avec Senprof (nouvelle fenêtre)