INTRODUCTION⚓
Les vecteurs sont des outils fondamentaux en mathématiques. Ils permettent de représenter des grandeurs qui possèdent à la fois une intensité, une direction et un sens. De par leurs représentation et propriétés ils nous aident à manipuler les informations vectorielles, à visualiser et comprendre les déplacements, les forces. Leur étude est essentielle pour résoudre des problèmes pratiques dans divers domaines.
Rappels⚓
Caractéristiques d'un vecteur
Les caractéristiques d'un vecteur sont sa direction, son sens et sa longueur
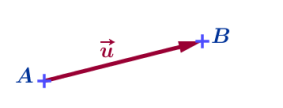
La figure ci contre représente le vecteur \(\overrightarrow{u}=\overrightarrow{AB}\)
sa direction est celle de la droite (AB)
son sens: de \(A\) vers \(B\) c'et à dre le sens de la demi droite \([AB)\)
sa longueur: \(AB\)
Vecteurs égaux
Deux vecteurs sont égaux lorsqu'ils ont la même direction, le même sens et la même longueur
Définition : Vecteurs opposés
Deux vecteurs sont opposés lorsqu'ils ont la même direction, la même longueur et des sens contraires
L'opposé du vecteur \(\overrightarrow{AB}\) est le vecteur \(-\overrightarrow{AB}\). On a : \(-\overrightarrow{AB}=\overrightarrow{BA}\)
teste toi⚓
Question⚓
Addition vectorielle⚓
Vecteur somme de deux vecteurs⚓
Définition :
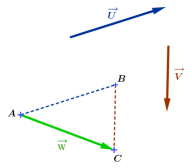
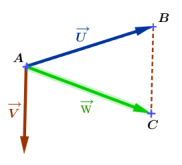
Soient \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs.
Pour tout point \(A\) du plan, si \(C\) est l'image de \(A\) par la translation de vecteur \(\overrightarrow{u}\) suivi de la translation de vecteur \(\overrightarrow{v}\) alors le vecteur \(\overrightarrow{w}=\overrightarrow{AC}\) est le vecteur somme de \(\overrightarrow{u}\) et \(\overrightarrow{v}\).
Nota Bene :
La somme des vecteurs est indépendante de la position du point \(A\). On peut choisir par conséquent l'origine de l'un des vecteurs, ce qui permet de faire une construction simple.
Relation de Chasles⚓
Propriété
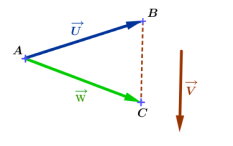
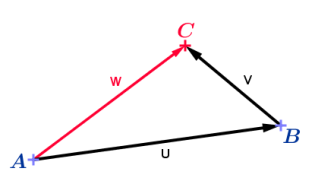
Si \(A, B\) et \(C\) sont trois points du plan, on a la relation \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\) .Cette relation peut s'ecrire dans l'autre sens \(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\).
c'est la relation de Chasles. Cette relation peut permettre de reduire une somme de vecteurs.
Exemple :
Réduis la somme vectorielle suivante: \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CH}\)
On a :
\(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CH}=\overrightarrow{AC}+\overrightarrow{CH}=\overrightarrow{AH}\)
\(\)
Vecteurs opposés⚓
Nota Bene :
La somme d'un vecteur et son opposé est égal au vecteur nul. \(\overrightarrow{AB}+\overrightarrow{BA}=\overrightarrow{BB}=\overrightarrow{0}\)
Multiplication d'un vecteur par un nombre réel⚓
Vecteur produit d'un vecteur par un nombre réel⚓
Définition :
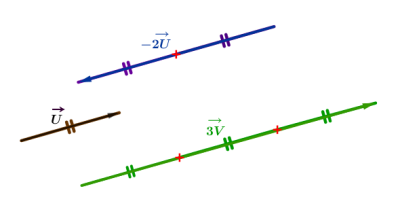
Soient \(\overrightarrow{u}=\overrightarrow{AB}\) un vecteur et \(k\) un nombre réel non nul. Le vecteur \(k\overrightarrow{u}\) a :
la même direction que le vecteur \(\overrightarrow{u}\)
le mêmes sens que \(\overrightarrow{u}\) si \(k\) est positif et le sens contraire de celui de \(\overrightarrow{u}\) si \(k\) est négatif.
pour longueur :.\(\left|a\right|\times{AB}\)
Configurations⚓
Exemple :
Sur la figure ci-contre, sont représentés les vecteurs \(\overrightarrow{u}\),\(-2\overrightarrow{v}\) et \(3\overrightarrow{u}\)
Vecteurs colinéaires⚓
Définition :
Deux vecteurs sont colinéaires s'ils ont la même direction ou si l'un d'eux est nul.
Exemple:
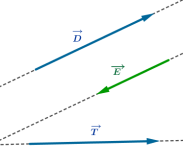
Sur la figure ci contre les vecteurs \(\overrightarrow{D}\) et \(\overrightarrow{E}\) sont colinéaires et les vecteurs \(\overrightarrow{D}\) et \(\overrightarrow{T}\) ne sont pas colinéaires.
Teste toi.
Propriétés
Soient \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs.
Si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires alors il existe un nombre réel \(k\) tel que \(\overrightarrow{u}=k\overrightarrow{v}\)
S'il existe un nombre réel \(k\) tel que \(\overrightarrow{u}=k\overrightarrow{v}\) alors \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires.
Exemple :
Soient les vecteurs \(\overrightarrow{u}\) , \(\overrightarrow{f}\) et \(\overrightarrow{h}\)
les vecteurs \(\overrightarrow{u}\) et \(7\overrightarrow{u}\) sont colineaires.
\(2\overrightarrow{f}\) et \(-3\overrightarrow{h}\) sont deux vecteurs colineaires car on peut écrire \(\overrightarrow{f}=-\dfrac{3}{2}\overrightarrow{h}\)
Question⚓
On donne \(\overrightarrow{r}=5\overrightarrow{g}\) et \(\overrightarrow{g}=3\overrightarrow{h}\)
Montre que les vecteurs \(\overrightarrow{r}\) et \(\overrightarrow{h}\) sont colineaires
Colinéarité et parallélisme
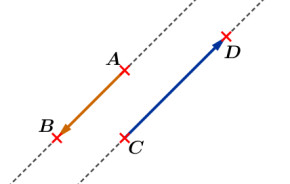
Soient \(A\),\( B\), \(C\) et \(D\) quatre points distincts du plan.
Si les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) sont colinéaires alors les droites \((AB)\) et \((CD)\) sont parallèles
Si les droites \((AB)\) et \((CD)\) sont parallèles alors les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) sont colinéaires.
Colinéarité et alignement
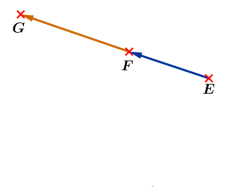
Soient \(E\),\(F\) et \(G\) trois points du plan:
Si les vecteur \(\overrightarrow{EF}\) et \(\overrightarrow{EG}\)sont colinéaires alors les points \(E\), \(F\) et \(G\) sont alignés
Si les points \(E,~F\) et \(G\) sont alignés alors les les vecteurs \(\overrightarrow{EF}\) et \(\overrightarrow{EG}\) sont colinéaires.
Question⚓
On donne dans le plan les points \(A\), \(B\), \(KL\) et \(M\) des points du plan tels que:
\(\overrightarrow{KL}=-2\overrightarrow{AB}\) et \(3\overrightarrow{AB}=5\overrightarrow{KM}\)
Ecris le vecteurs \(\overrightarrow{KL}\) à l'aide de \(\overrightarrow{KM}\)
Justife que les points \(K\), \(L\), et \(M\) sont alignés.
Solution⚓
\(3\overrightarrow{AB}=5\overrightarrow{KM}\) équivaut à \(\overrightarrow{AB}=\dfrac{5}{3}\overrightarrow{KM}\). On obtient \(\overrightarrow{KL}=-2\overrightarrow{AB}\) =\(-2(\dfrac{5}{3}\overrightarrow{KM})\) ce qui donne \(\overrightarrow{KL}=-\dfrac{10}{3}\overrightarrow{KM}\).
On a : \(\overrightarrow{KL}=k\times\overrightarrow{KM}\) avec \(k=-\dfrac{10}{3}\) donc les vecteurs \(\overrightarrow{KL}\) et \(\overrightarrow{KM}\) sont colineaires d'où les points \(K\), \(L\), et \(M\) sont alignés.