Primitives et Intégrales

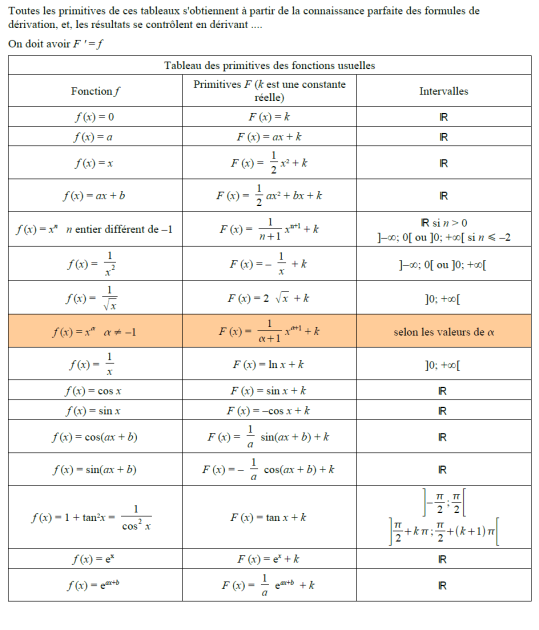
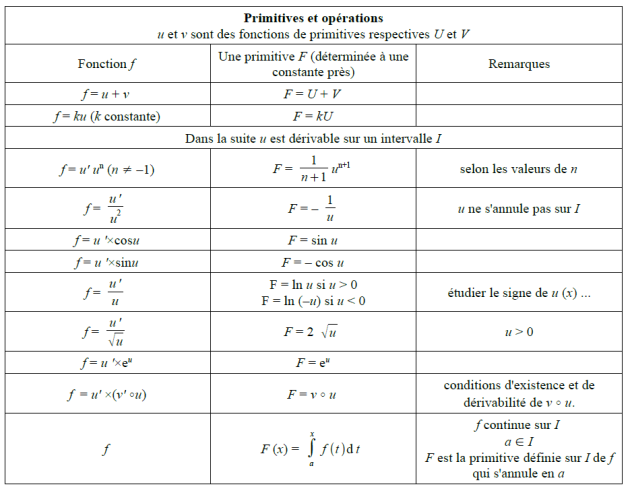
Définition : Généralités

Soit \(f:[a,b]\to\mathbb{R}\) une fonction. On dit qu'une fonction \(F:[a,b]\to\mathbb{R}\) est une primitive de \(f\) si

\(F\) est continue sur \([a,b]\),
\(F\) est dérivable sur \(]a,b[\) et \(F'(x)=f(x)\) pour tout \(x\in]a,b[\).

Méthode : Proposition

Deux primitives d'une même fonction \(f:[a,b]\to\mathbb{R}\) diffèrent d'une constante.
Soit \(f:[a,b]\to\mathbb{R}\) une fonction continue. Posons \(F(x)=\displaystyle\int_{a}^{x}f(t)\,\mbox{d}t\). Alors \(F\) est l'unique primitive de \(f\) qui s'annule en \(a\).

Définition :

Soit \(f:[a,b]\to\mathbb{R}\) une fonction continue et \(F\) une primitive de \(f\). Alors on définit l'intégrale de \(a\) à \(b\) de \(f\) par le nombre \(F(b)-F(a)\). On la note par \(\displaystyle\int_{a}^{b}f(t)\,{\rm d}t\).

Ainsi on a \(\displaystyle\int_{a}^{b}f(t)\,{\rm d}t=F(b)-F(a)=[F(t)]^b_a\) (par notation).

Complément : Primitives usuelles

Exemple : Calcul de primitives (intégration à vue)

\(\displaystyle\int\left(x+\dfrac 1x\right)^2{\rm d}x=\displaystyle\int\left(x^2+2+\dfrac 1{x^2}\right){\rm d}x=\dfrac{x^3}3+2x-\dfrac 1x+K,\ K\in\mathbb R\).
\(\displaystyle\int (2x+3)(x^2+3x+5)^3{\rm d}x=\dfrac 14(x^2+3x+5)^4+K,\ K\in\mathbb R\). Dans ce cas de figure il serait maladroit de développer, l'expression est de la forme \(u'\cdot u^n\) avec \(n=3\).
\(\displaystyle\int\sin x{\rm e}^{\cos x}{\rm d}x=-{\rm e}^{\cos x}+K,\ K\in\mathbb R\). L'expression est de la forme \(u'{\rm e}^u\).

Pour plus d'informations veuillez visionner la vidéo

Intégration par parties ⚓

Méthode :

Soient \(u:[a,b]\to\mathbb{R}\) et \(v:[a,b]\to\mathbb{R}\) deux fonctions dérivables telles que \(\int_{a}^{b}u'(x)v(x)\mbox{d}x\ \textrm{ et } \int_{a}^{b}u(x)v'(x)\mbox{d}x\) existent. Alors on a l'égalité :

\(\int_{a}^{b}u(x)v'(x)\mbox{d}x+\int_{a}^{b}u'(x)v(x)\mbox{d}x=[u(x)v(x)]^b_a=u(b)v(b)-u(a)v(a)\)

Exemple : Calcul de primitives en Intégrant par parties

\(\displaystyle\int\ln x{\rm d}x\). Pour déterminer de telles primitives, on pose \(\begin{cases} u'=1,\qquad u=x \\ v=\ln x, \qquad v'=\dfrac 1x\end{cases}\) d'où \(\displaystyle\int\ln x{\rm d}x=x\ln x-\displaystyle\int 1{\rm d}x=x\ln x-x+k,\ k\in\mathbb R\).

\(\displaystyle\int x\sin x{\rm d}x\) on pose \(\begin{cases} u'=\sin x,\qquad u=-\cos x \\ v= x, \qquad v'=1\end{cases}\) d'où \(\displaystyle\int x\sin x{\rm d}x=-x\cos x+\displaystyle\int \cos x{\rm d}x=-x\cos x+\sin x+K,\ K\in \mathbb R\).

Pour voir un exemple de résolution, visionner la vidéo ci-dessous

Changement de variables ⚓

Soit \(u:[a,b]\to\mathbb{R}\) une fonction affine. Soit \(u[a,b]=I\). Considérons une fonction continue \(f:I\to\mathbb{R}\).

On a l'égalité \(\displaystyle\int_{u(a)}^{u(b)}f(x)\mbox{d}x=\displaystyle\int_{a}^{b}f(u(x)).u'(x)\mbox{d}x\)

Exemple :

Calcul l'intégrale suivante : \(\displaystyle\int_0^{\frac\pi 2}\cos (2x+\pi/2){\rm d}x\).

\(\displaystyle\int_0^{\frac\pi 2} \cos(2x+\pi/2){\rm d}x=\dfrac 12\displaystyle\int_{\frac\pi 2}^{\frac{3\pi} 2}\cos(u){\rm d}u=\dfrac 12[\sin(x)]^{\frac{3\pi} 2}_\frac\pi 2=-1\)

Quelques méthodes et techniques ⚓

Exemple : Primitives de quelques fonctions rationnelles

La fonction \(\frac{1}{x-a}\) admet pour primitive la fonction \(\ln(\vert x-a\vert)\) sur tout intervalle ne contenant pas \(a\).
La fonction \(\dfrac{1}{x{}^{n}}, \ (n>1)\) admet pour primitive la fonction \(\dfrac{-1}{(n-1)x^{n-1}}\) sur tout intervalle ne contenant pas \(a\).
La fonction \(\dfrac{2x}{x^{2}+1}\) admet pour primitive la fonction \(\ln(x^{2}+1)\) sur tout intervalle.
La fonction \(\dfrac{1}{x^{2}+1}\) admet pour primitive la fonction \(\arctan(x)\) sur tout intervalle.
La fonction \(\dfrac{2x}{\left(x^{2}+1\right)^{n}}\) admet pour primitive la fonction \(\dfrac{-1}{(n-1)(x^{2}+1)^{n-1}}\) sur tout intervalle.
Posons \(F_{1}(x)=\arctan(x)\) et pour \(n\geq1\), \(F_{n+1}(x)=\dfrac{x}{2n(1+x^{2})^{n}}+\dfrac{2n-1}{2n}F_{n}(x)\). Alors la fonction \(F_{n}\) est une primitive de la fonction \(\dfrac{1}{(x^{2}+1)^{n}}\) sur tout intervalle.