Les distributions statistiques à deux dimensions⚓
Définition :
Considérons une population de taille \(n\) notée \(\Omega\) . Si on étudie deux caractères \(X\) et \(Y\) de cette population, on dit que
l'on étudie une série statistique double. La Statistique bivariée (à 2 dimension) est une application
\(\begin{eqnarray*} (X, Y ) :\, & \Omega&\rightarrow \mathbb{R}\\&\omega&\mapsto (X(\omega), Y (\omega)).\end{eqnarray*}\)
Tableau de contingence, distributions marginales et conditionnelles⚓
Considérons un échantillon de \(n\) individus sur lequel nous observons deux variables quantitatives
\(\textcolor{white}{\cdot} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad X = \{x_{1}, x_{2}, . . . , x_{k}\}\)
et
\(\textcolor{white}{\cdot} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad Y = \{ y_{1}, y_{2}, . . . , y_{l}\}\)
ayant respectivement \(k\) et \(l\) modalités.
A chaque couple \((x_{i} ,y_{j})\) correspond une case du tableau statistique à double entrées, où figurent en lignes les modalités de \(X\) et en colonnes les modalités de \(Y\) . Le nombre d'éléments présentant à la fois les modalités \(x_{i}\) et \(y_{j}\) est l'effectif du couple \((x_{i} ,y_{j})\) que l'on note \(n_{i j}\).
\(X\backslash Y\) | \(y_{1}\) | \(\cdots\) | \(y_{j}\) | \(\cdots\) | \(y_{l}\) | Totaux en ligne |
\(x_{1}\) | \(n_{11}\) | \(\cdots\) | \(n_{1j}\) | \(\cdots\) | \(n_{1l}\) | \(n_{1.}\) |
\(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) |
\(x_{i}\) | \(n_{i1}\) | \(\cdots\) | \(n_{ij}\) | \(\cdots\) | \(n_{il}\) | \(n_{i.}\) |
\(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) | \(\cdots\) |
\(x_{k}\) | \(n_{k1}\) | \(\cdots\) | \(n_{kj}\) | \(\cdots\) | \(n_{kl}\) | \(n_{k.}\) |
Totaux en colonne | \(n_{.1}\) | \(\cdots\) | \(n_{.j}\) | \(\cdots\) | \(n_{.l}\) | \(n_{..}\) |
Les quantités \(n_{ij}\) sont appelées les effectifs conjoints.
Le tableau de contingence représente la distribution conjointe du couple \((X, Y)\).
Les quantités \(n_{i.}\) \((i=1,...,k)\) et \(n_{.j}\) \((j=1,...,l)\), appelées effectifs marginaux, sont définies de la façon suivante:
\(\textcolor{white}{\cdot} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad n_{i.}=\displaystyle\sum_{j=1}^{l}n_{ij}; \quad \quad n_{.j}=\displaystyle\sum_{i=1}^{k}n_{ij}.\)
Elles vérifient
\(\textcolor{white}{\cdot} \quad\quad\quad\quad \quad\quad\quad\quad\quad\quad\quad\quad \displaystyle\sum_{i=1}^{k}n_{i.}=\displaystyle\sum_{j=1}^{l}n_{.j}=n=n_{..}.\)
Définition : Fréquence conjointe
On appelle fréquence (conjointe) du couple \((x_{i}, y_{j} )\) la proportion des observations qui présentent simultanément les modalités \(x_{i}\) et \(y_{j} \)notée par
\(\textcolor{white}{\cdot} \quad\quad\quad\quad \quad\quad\quad\quad\quad\quad\quad\quad\quad f_{ij}=\displaystyle\frac{n_{ij}}{n}.\)
Définition : Distributions marginales
On appelle distributions marginales les totaux des fréquences relatives aux différentes lignes et colonnes, c'est-à-dire :
\(\textcolor{white}{\cdot} \quad\quad \quad\quad\quad\quad \quad\quad\quad\quad f_{i.}=\displaystyle\sum_{j=1}^{l}f_{ij}=\displaystyle\sum_{j=1}^{l}\displaystyle\frac{n_{ij}}{n}=\displaystyle\frac{n_{i .}}{n}.\)
\(f_{i.}\) est la somme des fréquences de la ligne \(i\).
\(\textcolor{white}{\cdot} \quad\quad\quad\quad\quad\quad \quad\quad\quad\quad f_{.j}=\displaystyle\sum_{i=1}^{k}f_{ij}=\displaystyle\sum_{i=1}^{k}\displaystyle\frac{n_{ij}}{n}=\displaystyle\frac{n_{.j}}{n}.\)
\(f_{.j}\) est la somme des fréquences de la colonne \(j\).
Définition : Distributions conditionnelles
Les effectifs (ou fréquences) de la ligne \(i\) définissent la distribution selon la variable \(Y\) des \(n_{i.}\) individus.
Cette distribution est la distribution conditionnelle de \(Y\) sachant que \(X=x_{i}\).
Il y a \(k\) distributions conditionnelles de \(Y\) pour \(X= x_{i}\); \(i=1,...,k\).
Les effectifs (ou fréquences) de la colonne \(j\) définissent la distribution selon la variable \(X\) des \(n_{.j}\) individus.
Cette distribution est la distribution conditionnelle de \(X\) sachant que \(Y=y_{j}\).
Il y a \(l\) distributions conditionnelles de \(X\) pour \(Y= y_{j}\); \(j=1,...,l\).
Exemple :
On a réparti \(1000\) individus d'une population suivant
le nombre \(x\) d'arrêts de travail suite à des accidents par an,
l'âge \(y\) en années de ces individus.
On obtient les résultats synthétisés dans le tableau ci-dessous.
\(x_{i}\backslash y_{j}\) | \([20,30[\) | \([30 , 40[\) | \([40, 50[\) | \([50, 60[\) | \(n_{i.}\) |
0 | 20 | 150 | 22 | 0 | 192 |
1 | 99 | 102 | 180 | 12 | 393 |
2 | 60 | 51 | 150 | 30 | 291 |
3 | 18 | 0 | 50 | 32 | 100 |
4 | 3 | 0 | 10 | 11 | 24 |
\(n_{.j}\) | 200 | 303 | 412 | 85 | 1000 |
Les distributions marginales de \(X\) et \(Y\) en termes d'effectifs sont respectivement :
\(x_{i}\) | 0 | 1 | 2 | 3 | 4 | Total |
\(n_{i.}\) | 192 | 393 | 291 | 100 | 24 | 1000 |
\(y_{j}\) | [20,30[ | [30,40[ | [40,50[ | [50,60[ | Total |
\(n_{.j}\) | 200 | 303 | 412 | 85 | 1000 |
La distribution conditionnelle de \(Y\) sachant que \(X=2\) est donnée par
\(y_{j}\) | \([20,30[\) | \([30 , 40[\) | \([40, 50[\) | \([50, 60[\) | Total |
\(Y/X=2\) | 60 | 51 | 150 | 30 | 291 |
La distribution conditionnelle de \(X\) sachant que \(Y\in[20,30[\) est donnée par
\(x_{i}\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | Total |
\(X/Y\in[20,30[\) | 20 | 99 | 60 | 18 | 3 | 200 |
Indépendance statistique⚓
On dit que les variables \(X\) et \(Y\) sont indépendantes si, et seulement si :
\(f_{ij} =f_{i.}\times f_{.j}\) ou \(n_{ij} =\displaystyle\frac{n_{i.}n_{.j}}{n}\), \(\forall i = 1, . . . , k\) et \(\forall j = 1, . . . , l\).
Attention :
La connaissance des distributions marginales de \(X\) et de \(Y\) ne suffit pas, en général, pour déterminer la distribution du couple\( (X, Y )\) sauf si \(X\) et \(Y\) sont indépendantes.
Etude conjointe de deux variables quantitatives⚓
Deux variables quantitatives \(X\) et \(Y\) sont observées chez \(n\) individus d'une population.
Par exemple, \(X\) peut désigner le poids et \(Y\) la taille. Les deux séries de données peuvent être représentées conjointement sous la forme d'une série statistique double \(\{(x_{1},y_{1}), (x_{2},y_{2}),...,(x_{i},y_{i}),...,(x_{n},y_{n})\}\).
Ici, la notation \((x_{i},y_{i})\) désigne le couple de valeurs obtenues en observant le poids \(x_{i}\) et la taille \(y_{i}\) chez l'individu \(i\).
\(x_{i}\) est la valeur de \(X\) pour l'individu \(i\). \(y_{i}\) est la valeur de \(Y\) pour l'individu \(i\).
Nuage de points⚓
Pour étudier l'intensité de la liaison entre deux variables quantitatives \(X\) et \(Y\) observées sur \(n\) individus, le graphique habituel est le nuage de points (ou diagramme de dispersion).
Il fait correspondre à chaque couple \((x_{i},y_{i})\) un point d'abscisse \(x_{i}\) et d'ordonnée \(y_{i}\) dans un repère cartésien.
Ce graphique permet de voir si les points sont groupés autour d'une droite ou d'une courbe, ou s'ils sont totalement dispersés.
Exemple :
Considérons les séries d'observations sur les bateaux utilisés (variable \(X\)) et la prise effectuée (variable \(Y\)) par une pêcherie artisanale.
Jour | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Nombre de bateaux (x) | 12 | 15 | 10 | 12 | 18 | 14 | 6 | 15 | 16 | 9 |
Prise totale (kg) | 590 | 820 | 330 | 740 | 900 | 660 | 240 | 650 | 850 | 470 |
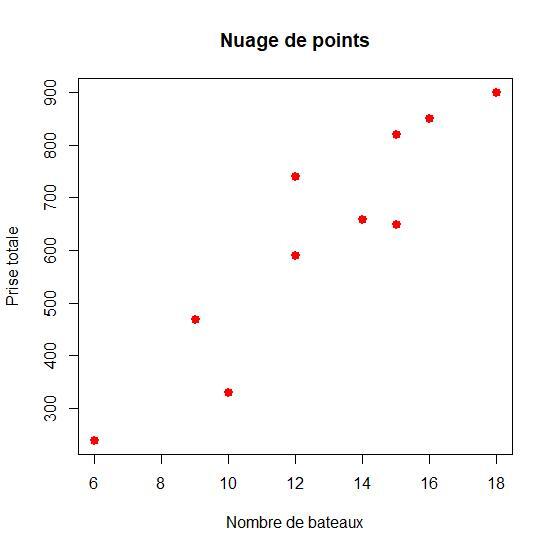
Le point moyen du nuage est représenté en bleu sur la figure.
Description numérique⚓
Caractéristique des séries marginales⚓
Dans le cas d'une variable statistique à deux dimensions \(X\) et \(Y\), les moyennes marginales sont données respectivement par
\(\overline{x}=\displaystyle\frac{1}{n}\displaystyle\sum_{i=1}^{k}n_{i.}x_{i}=\displaystyle\sum_{i=1}^{k}f_{i.}x_{i},\quad \quad \overline{y}=\displaystyle\frac{1}{n}\displaystyle\sum_{j=1}^{l}n_{.j}y_{j}=\displaystyle\sum_{j=1}^{l}f_{.j}y_{j}.\)
Si \(X\) (resp. \(Y\)) est continu, on remplace \(x_{i}\) (resp.\(y_{j}\)) par le centre de la classe de \(X\) (resp. \(Y\)) .
Nous définissons maintenant la variance marginale de \(X\) et la variance marginale de \(Y\) comme suit:
\(\sigma^{2}_{X}=var(X)=\displaystyle\frac{1}{n}\displaystyle\sum_{i=1}^{k}n_{i.}(x_{i}-\overline{x})^{2}=\displaystyle\frac{1}{n}\displaystyle\sum_{i=1}^{k}n_{i.}x_{i}^{2}-(\overline{x})^{2}.\)
\(\sigma^{2}_{Y}=var(Y)=\displaystyle\frac{1}{n}\displaystyle\sum_{j=1}^{l}n_{.j}(y_{j}-\overline{y})^{2}=\displaystyle\frac{1}{n}\displaystyle\sum_{j=1}^{l}n_{.j}y_{j}^{2}-(\overline{y})^{2}.\)
Exemple :
Nous calculons \(\overline{x}\), \(\overline{y}\), \(\sigma_{X}\) et \(\sigma_{Y}\) pour l'exemple précédent.
x | 12 | 15 | 10 | 12 | 18 | 14 | 6 | 15 | 16 | 9 |
y | 590 | 820 | 330 | 740 | 900 | 660 | 240 | 650 | 850 | 470 |
\(\overline{x}=\displaystyle\frac{1}{10}\displaystyle\sum_{i=1}^{10}x_{i}=\displaystyle\frac{1}{10}(12+15+10+12+18+14+6+15+16+9)=12,7.\)
\(\begin{eqnarray*}var(X) &=& \displaystyle\frac{1}{10}\displaystyle\sum_{i=1}^{10}x_{i}^{2}-(\overline{x})^{2}\\&=&\displaystyle\frac{1}{10}(12^{2}+15^{2}+10^{2}+12^{2}+18^{2}+14^{2}+6^{2}+15^{2}+16^{2}+9^{2})-12,7^{2}\\&=& 11,81\\ \end{eqnarray*}\)
\(\sigma_{X}=\sqrt{var(X)}=3,44.\)
\(\overline{y}=\displaystyle\frac{1}{10}\displaystyle\sum_{i=1}^{10}y_{i}=\displaystyle\frac{1}{10}(590+820+330+740+900+660+240+650+850+470)=625.\)
\(\begin{eqnarray*}var(Y) &=& \displaystyle\frac{1}{10}\displaystyle\sum_{i=1}^{10}y_{i}^{2}-(\overline{y})^{2}\\&=&\displaystyle\frac{1}{10}(590^{2}+820^{2}+330^{2}+740^{2}+900^{2}+660^{2}+240^{2}+650^{2}+850^{2}+470^{2})\\& & -625^{2}\\&=&43985\\ \end{eqnarray*}\)
\(\sigma_{Y}=\sqrt{var(Y)}=209,726\).
Notion de covariance⚓
Nous notons par \(cov(X, Y )\) la covariance entre les variables \(X\) et \(Y.\) La covariance est un paramètre qui étudie la variabilité de \(X\) par rapport à \(Y\). Son expression est donnée par la formule suivante :
\(cov(X,Y)=\displaystyle\frac{1}{n}\displaystyle\sum_{i=1}^{k}\displaystyle\sum_{j=1}^{l}n_{ij}(x_{i}-\overline{x})(y_{j}-\overline{y})=\displaystyle\frac{1}{n}\displaystyle\sum_{i=1}^{k}\displaystyle\sum_{j=1}^{l}n_{ij}x_{i}y_{j}-\overline{x}.\overline{y}.\)
Attention :
Dans le cas d'une série statistique double du type \(\{(x_{1},y_{1}), (x_{2},y_{2}),...,(x_{i},y_{i}),...,(x_{n},y_{n})\}\), la covariance s'écrit:
\(cov(X,Y)=\displaystyle\frac{1}{n}\displaystyle\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})=\displaystyle\frac{1}{n}\displaystyle\sum_{i=1}^{n}x_{i}y_{i}-\overline{x}.\overline{y}.\)
Exemple :
Pour
x | 12 | 15 | 10 | 12 | 18 | 14 | 6 | 15 | 16 | 9 |
y | 590 | 820 | 330 | 740 | 900 | 660 | 240 | 650 | 850 | 470 |
\(cov(x,y)=\displaystyle\frac{1}{n}\displaystyle\sum_{i=1}^{n}x_{i}y_{i}-\overline{x}.\overline{y}\)
\(=\displaystyle\frac{1}{10}(12\times590+15\times820+10\times330+12\times740+18\times900+14\times660+6\times240+15\times650+\)
\(16\times850+9\times470)-12,7\times625\)
\(=664,5.\)
Régression et corrélation⚓
Dans le cas où l'on peut mettre en évidence l'existence d'une relation linéaire significative entre deux variables quantitatives \(X\) et \(Y\) (le nuage de points est alors allongé), on peut chercher à formaliser la liaison entre ces deux variables à l'aide d'une équation de droite. Cette démarche est appelée ajustement linéaire.
Le coefficient de corrélation linéaire⚓
Définition :
Le coefficient de corrélation linéaire est la covariance divisée par le produit des deux écart-types marginaux. On le note \(r_{X,Y}\) ou tout simplement \(r\) s'il n' y a pas d’ambiguïté sur les variables:
\(\textcolor{white}{\cdot} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad r_{X,Y}=\displaystyle\frac{cov(X,Y)}{\sigma_{X}\sigma_{Y}}.\)
Complément :
\(-1\leq r_{X,Y} \leq 1\).
Remarques
Le coefficient de corrélation permet d'apprécier l'intensité de la liaison linéaire entre les deux variables \(X\) et \(Y\):
\(| r_{X,Y}|=1\) est équivalent à l'existence d'une relation linéaire exacte entre les deux variables.
Si le coefficient de corrélation est positif, les points sont alignés le long d'une droite croissante.
Si le coefficient de corrélation est négatif, les points sont alignés le long d'une droite décroissante.
Si le coefficient de corrélation est nul ou proche de zéro, il n'y a pas de dépendance linéaire. On peut cependant avoir une dépendance non linéaire avec un coefficient de corrélation nul.
Plus précisément il est d'usage de considérer que:
\(0,95 \leq \mid r_{X,Y} \mid \leq 1\) correspond à une très forte corrélation.
\(0,70 \leq \mid r_{X,Y} \mid < 0,95\) correspond à une forte corrélation.
\(\mid r_{X,Y} \mid < 0,70\) correspond à une faible corrélation.
Droite des moindres carrés de Y en X⚓
Soit un ensemble de \(n\) observations \((x_{i},y_{i})\), \(i=1,\cdots,n\) de deux variables quantitatives \(X\) et \(Y\).
\(X\) est la variable explicative.
\(Y\) est la variable estimée (ou expliquée) qui est liée linéairement à \(X\).
Lorsque l'on dispose d'un nuage de points qui a un aspect linéaire, on peut essayer de tracer "à main levée" la droite d'équation \(Y=aX+b\) qui caractérise ce nuage et lire graphiquement les valeurs de \(a\) et \(b\).
Cette méthode peu objective est rarement utilisée.
La méthode des moindres carrées est souvent utilisée pour estimer \(a\) et \(b\).
La régression de \(Y\) en \(X\) postule que la connaissance des valeurs de \(X\) permet de prévoir celles de \(Y\). Il s'agit donc de prévision et l'objectif est de minimiser l'erreur de prévision c'est-à-dire l'écart entre les valeurs observées de \(Y\) et les valeurs estimées de \(Y\) par la relation \(Y=aX+b\). Les erreurs seront donc les distances à la droite par rapport à l'axe des ordonnées.
En observant le figure ci-dessous pour illustration, on constate que lorsque l'on cherche à exprimer \(Y\) en fonction de\( X\), on peut affecter à chaque valeur observée \(y_{i}\) une valeur estimée par la droite de régression . L'erreur d'estimation sur l'individu \(i\) est donc représentée par un segment vertical qui joint les deux points.
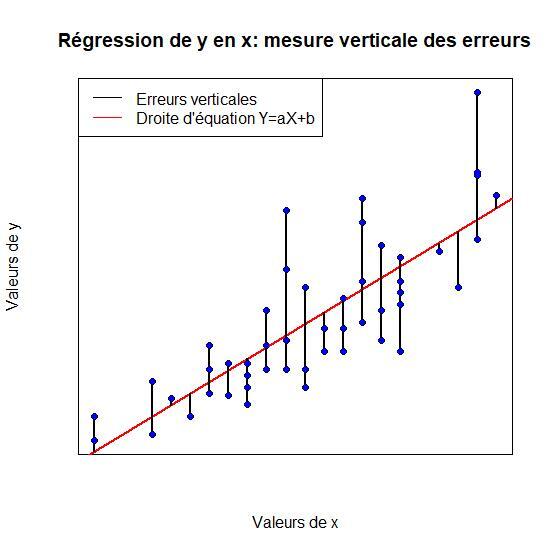
Comme on souhaite obtenir un ajustement optimal, il faut définir un critère général définissant la qualité d'ajustement de l'ensemble des valeurs à la droite proposée.
La première solution qui vient à l'esprit est la minimisation de la somme des erreurs. Ce critère est discutable car des erreurs positives et négatives peuvent se compenser et l'on pourrait obtenir un ajustement optimal sans même que la droite ne passerait pas par tous les points du nuage.
La solution qui est la plus souvent retenue en statistique est appelée critère des moindres carrés et consiste à minimiser de la somme des carrés des erreurs. Ce critère est apparemment correct car il n'y a pas de compensation entre les erreurs positives et négatives.
L'équation de la droite de régression Y=aX+b qui minimise le carré des écarts entre valeurs observées et valeurs estimées est obtenue à l'aide des deux formules suivantes :
La droite des moindres carrés (ou de régression) de \(Y\) en \(X\) a donc pour équation: \(\textcolor{white}{\cdot} \quad\quad\quad\quad D_{Y/X}: Y=aX+b,\quad \hbox{avec}\,\,a=\displaystyle\frac{cov(X,Y)}{var(X)}\quad\quad\hbox{et}\,\, b=\overline{Y}-a\overline{X}.\)
Droite des moindres carrés de X en Y⚓
La régression de \(X\) en Y part inversement du fait que les valeurs de \(X\) dépendent de celles de \(Y\), c'est-à-dire postule que la connaissance des valeurs de \(Y\) permet de prévoir celles de \(X\). Cette fois-ci, il s'agit donc de minimiser l'erreur de prévision sur \(X\) c'est-à-dire la distance entre les valeurs observées de \(X\) et les valeurs estimées de \(X\) par la relation \(X=a'Y+b'\). Les erreurss seront donc la distance à la droite par rapport à l'axe des abscisses et non plus par rapport à l'axe ordonnées comme précédemment.
En observant le figure ci-dessous pour illustration, on constate que lorsque l'on cherche à exprimer \(X\) en fonction de \(Y\), on peut affecter à chaque valeur observée \(x_{i}\) une valeur estimée par la droite de régression . L'erreur d'estimation sur l'individu \(i\) est donc égal au segment horizontal qui joint les deux points.
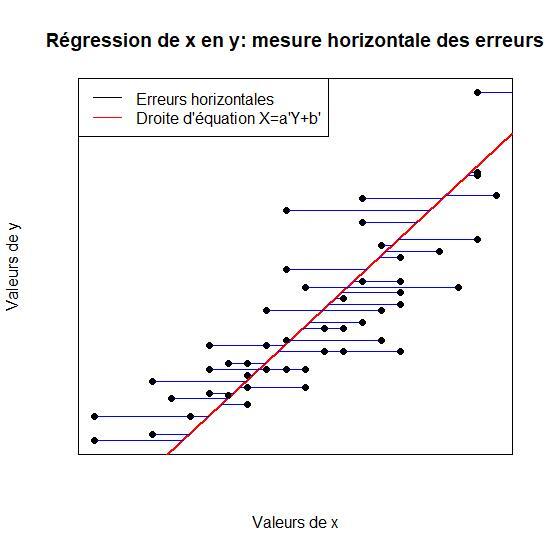
On suit une démarche analogue à celle qui a donné la droite des moindres carrés de \(Y\) en \(X\). On
cherche \`{a} ajuster une droite \(D_{X/Y}\) d'équation \(X=a'Y +b'\) au nuage de points.
On obtient la droite des moindres carrés de \(X\) en \(Y\):
\(\textcolor{white}{\cdot} \quad\quad\quad\quad D_{X/Y}: X=a'Y+b',\quad \hbox{avec}\,\,a'=\displaystyle\frac{cov(X,Y)}{var(Y)}\quad\quad\hbox{et}\,\, b'=\overline{X}-a'\overline{Y}.\)
Exemple :
Le tableau suivant donne pour 10 nouveaux-nés, numérotés de 1 à 10, la taille exprimée en cm, puis le poids, exprimé en kilogrammes:
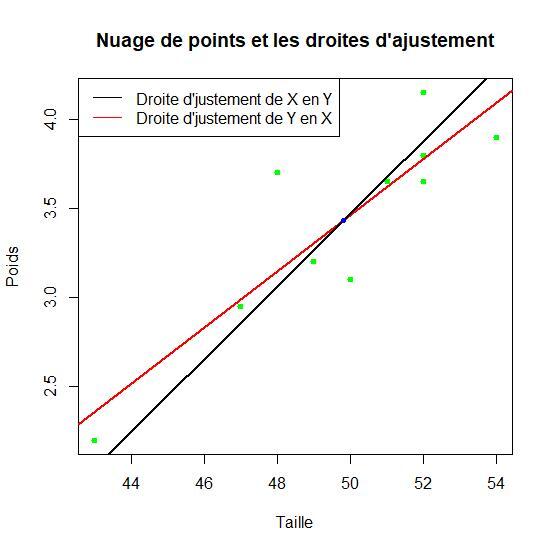
1) Construire le nuage de points représentant cette série double.
2) Calculer les coordonnées du point moyen du nuage.
3) Calculer le coefficient de corrélation linéaire. Un ajustement affine es-il justifié?
4) Construire les deux droites d'ajustement.
5) Estimer le poids d'un nouveau-né de 50 cm. Estimer la taille d'un nouveau-né de 3,1 kg.
\(\textbf{Solution}\)
Nous désignerons par \(X\) la taille et par \(Y\) le poids.
Voici le tableau de calcul qui contient toutes les informations numériques dont on aura besoin tout au long de l'exemple.
1)
\(x_{i}\) | \(y_{i}\) | \(x_{i}^{2}\) | \(y_{i}^{2}\) | \(x_{i}y_{i}\) |
52 | 3,65 | 2704 | 13,3225 | 189,80 |
48 | 3,7 | 2304 | 13,6900 | 177,60 |
51 | 3,65 | 2601 | 13,3225 | 186,15 |
54 | 3,9 | 2916 | 15,2100 | 210,60 |
50 | 3,1 | 2500 | 9,6100 | 155,00 |
49 | 3,2 | 2401 | 10,2400 | 156,80 |
47 | 2,95 | 2209 | 8,7025 | 138,65 |
52 | 3,8 | 2704 | 14,4400 | 197,60 |
52 | 4,15 | 2704 | 17,2225 | 215,80 |
43 | 2,2 | 1849 | 8,8400 | 94,60 |
\(\displaystyle\sum_{i=1}^{10}x_{i}=498\) | \(\displaystyle\sum_{i=1}^{10}y_{i}=498\) | \(\displaystyle\sum_{i=1}^{10}x_{i}^{2}=24892\) | \(\displaystyle\sum_{i=1}^{10}y_{i}^{2}=120,6\) | \(\displaystyle\sum_{i=1}^{10}x_{i}y_{i}=1722,6\) |
2) Désignons par \(G\) le point moyen du nuage, \(G(\overline{X},\overline{Y})\). Alors,
\(\overline{x}=\displaystyle\frac{1}{10}\sum_{i=1}^{10}x_{i}=49,8\); \(\overline{y}=\displaystyle\frac{1}{10}\sum_{i=1}^{10}y_{i}=3,43\) . Donc \(G(49,8;3,43)\).
3) \(r=\displaystyle\frac{cov(X,Y)}{\sigma_{X}.\sigma_{Y}}=0,8795002\) car \(cov(X,Y)=\displaystyle\frac{1}{10}\sum_{i=1}^{10}x_{i}y_{i}-\overline{X}.\overline{Y}\), \(\sigma_{X}=\displaystyle\sqrt{\displaystyle\frac{1}{10}\sum_{i=1}^{10}x_{i}^{2}-\overline{X}^{2}}\) et \(\sigma_{Y}=\displaystyle\sqrt{\displaystyle\frac{1}{10}\sum_{i=1}^{10}y_{i}^{2}-\overline{Y}^{2}}\).
\(0,70\leq| r |< 0,95\) correspond à une forte corrélation. Donc un ajustement affine est justifié.
4) Voir la figure précédente (Le point moyen du nuage, point d'intersection des deux droites d'ajustement est représenté en bleu sur la figure).
5) \(D_{Y/X}: Y=aX+b\), \(a=\displaystyle\frac{cov(X,Y)}{var(X)}= 0,1579\) et \(b=\overline{Y}-a\overline{X}=-4,4314\).
Donc \(D_{Y/X}: y=0,1579x -4,4314\).
Si \(x=50\), alors \(y=0,1579\times 50-4,4314=3,46.\)
On estime alors à \(3,46\) kg le poids d'un nouveau-né de 50 cm.
\(D_{X/Y}: X=a'Y+b'\), \(a'=\displaystyle\frac{cov(X,Y)}{var(Y)}= 4,9\) et \(b'=\overline{X}-a'\overline{Y}=32,99\).
Donc \(D_{X/Y}: x=4,9y+32,99 \).
Si \(y=3,1\), alors \(x=4,9\times 3,1+32,99=48,18.\)
On estime alors à \(48,18\) cm la taille d'un nouveau-né pesant \(3,1\) kg.