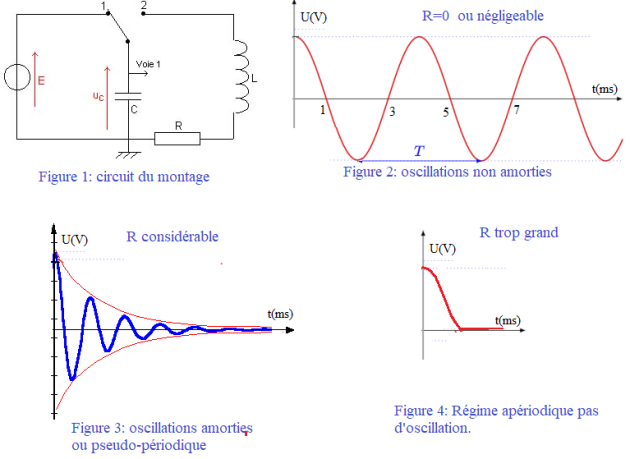
Oscillations électriques libres
La figure 1 représente un circuit R, L,C série. L'interrupteur en position 1 permet de charger le condensateur à partir d'un générateur de tension continu. Le condensateur chargé, l'interrupteur est basculé en position 2. Selon la valeur de la résistance, on observe à l'oscilloscope les courbes des figures 2, 3 ou 4.
Explications des oscillogrammes observés⚓
Figure 2
La figure 2 présente une sinusoïde parfaite qui traduit l'échange d'énergie entre la bobine et le condensateur.
Le condensateur initialement chargé se décharge progressivement sur la bobine qui emmagasine en même temps de l'énergie. A la fin de la décharge du condensateur, la bobine restitue progressivement l'énergie au condensateur. Et le phénomène se reproduit pratiquement sans perte d'énergie.
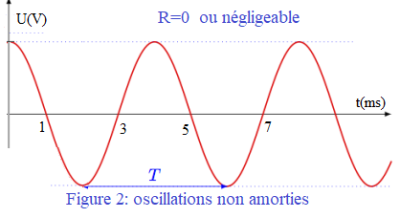
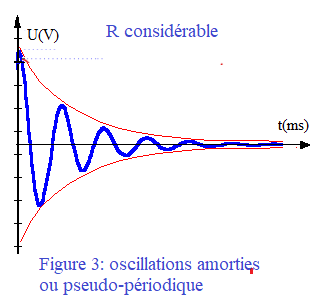
Figure 3
La figure 3 présente un amortissement des oscillations. La période des oscillations est la même mais l'amplitude décroît. Le système est amorti par la perte énergétique par effet joule due à la résistance électrique. Le régime est dit pseudo-périodique.
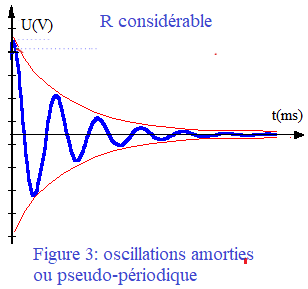
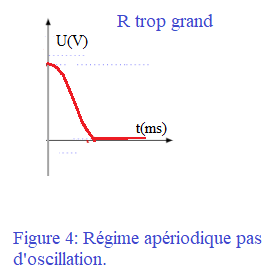
Figure 4
La figure 4 ne présente aucune oscillation. On a un amortissement important dû à la résistance électrique qui devient trop importante. Les pertes énergétiques par effet joule ne permettent pas un phénomène d'échange d'énergie entre le condensateur et la bobine. Le régime est apériodique.
Le régime pseudo-périodique et le régime apériodique sont distingués par une valeur particulière de la résistance appelée résistance critique notée \(R_c\).
Régime périodique ou non amorti.⚓
Equation différentielle par la loi des tensions
On exprime que la tension aux bornes du condensateur est égale à la tension aux bornes de la bobine en fixant un sens arbitraire de circulation du courant, voir figure ci-dessous. (on peut aussi écrire que la somme algébrique des tensions est nulle en parcourant la maille)
on a : \(u_c\)=\(u_L\) soit
\(\frac {q}{C} = \frac{Ldi}{dt}\)
En tenant compte de la relation suivante :
\(i=-\frac{dq}{dt}\), on obtient :
\(\frac {q}{C} =- \frac{Ld^2q}{dt^2}\) d'où l'équation différentielle :
\(\frac{Ld^2q}{dt^2}+\frac {q}{C}=0\)
ou encore
\(\frac{d^2q}{dt^2}+\frac {q}{LC}=\frac{d^2q}{dt^2}+\omega_0^2 q =0\)
\(\omega_0=\frac1{\sqrt{LC}}\) est la pulsation propre des oscillations.
\(T=\frac{2\pi}{\omega_0}\) est la période propre des oscillations (voir figure 2).
\(N_0=\frac1T\) est la période propre des oscillations.
Complément : Equation différentielle par la méthode énergétique
Nous exprimons la conservation de l'énergie totale E du système au cours du temps soit :
\(E=E_C+E_L\)
avec \(E_C\) l'énergie emmagasinée par le condensateur et \(E_L\) l'énergie emmagasinée par la bobine à la date t.
\(E=\frac {q^2}{2C}+\frac {Li^2}{2}\)
En annulant la dérivée par rapport au temps, en tenant compte de la relation \(i=\frac{dq}{dt}\) puis en simplifiant par l'intensité i du courant, on obtient l'équation différentielle :
\(\frac{Ld^2q}{dt^2}+\frac {q}{C}=0\)
Complément : Solution de l'équation différentielle
La solution de l'équation différentielle est de la forme :
\(q= A\cos (\omega_0.t+\phi )\)
\((\omega_0.t+\phi )\) est la phase des oscillations de la charge q,
\(\phi\) est la phase à l'origine des dates (t=0).
Rappel :
La tension électrique aux borne du condensateur est liée à la charge par la relation \(U_C=\frac{q}{C}\)
A vous de jouer
Question⚓
La variation de la charge du condensateur d'un circuit LC fermé avec une charge initiale \(q_0\) du condensateur peut être écrite sous la forme :
\(q= A\cos (\omega_0.t+\phi )\).
Déterminer A et \(\phi\).
Régime périodique amorti.⚓
Equation différentielle par la loi des tensions
Circuit électrique - Condensateur initialement chargé avec une charge \(q_0\) |
Oscillogramme observé à l'écran de l'oscilloscope |
A partir du circuit ci-dessus, nous pouvons écrire :
\(U_C+U_R=U_L\) soit
\(\frac {q}{C} -Ri= \frac{Ldi}{dt}\)
En tenant compte de la relation suivante :
\(i=-\frac{dq}{dt}\), on obtient :
\(\frac {q}{C} -R\frac{dq}{dt}= -\frac{Ld^2q}{dt^2}\) d'où l'équation différentielle :
\(\frac{Ld^2q}{dt^2}+R\frac{dq}{dt}+\frac {q}{C}=0\)
ou encore
\(\frac{d^2q}{dt^2}+\frac{R}{L}\frac{dq}{dt}+\frac {q}{LC}=\frac{d^2q}{dt^2}+2\lambda\frac{dq}{dt}+\omega_0^2 q =0\)
\(\omega_0=\frac1{\sqrt{LC}}\) est la pseudo-pulsation des oscillations.
\(T=\frac{2\pi}{\omega_0}\) est la pseudo-période des oscillations .
\(N_0=\frac1T\) est la pseudo-période des oscillations.
\(\lambda\) est le coefficient d'amortissement
Attention :
La pseudo-période et la période se déterminent graphiquement de la même manière. la notion de pseudo-période est relative à la forme de la courbe montrant une perte énergétique (diminution des amplitudes après chaque oscillation).
Complément : Equation différentielle par la méthode énergétique
Nous exprimons la non conservation de l'énergie totale E du système au cours du temps. L'énergie emmagasinée par le système est :
\(E=E_C+E_L\)
avec \(E_C\) l'énergie emmagasinée par le condensateur et \(E_L\) l'énergie emmagasinée par la bobine à la date t.
\(E=\frac {q^2}{2C}+\frac {Li^2}{2}\)
La dérivée par rapport au temps de l'énergie correspond à la puissance dissipée par effet joule dans le circuit.
conduit à l'expression :
\(\frac {dE}{dt}=\frac {q}{C}\frac{dq}{dt}+LI\frac {di}{dt}=-Ri^2\)
En tenant compte de la relation
\(i=\frac{dq}{dt}\)
puis en simplifiant par l'intensité i, on obtient :
puis en simplifiant par l'intensité i du courant, on obtient l'équation différentielle :
\(\frac{Ld^2q}{dt^2}+R\frac{dq}{dt}+\frac {q}{C}=0\)
Complément : Solution de l'équation différentielle
La solution de l'équation différentielle est de la forme :
\(q= A.e^{-\lambda.t}\cos (\omega_0.t+\phi )\)
\((\omega_0.t+\phi )\) est la phase des oscillations de la charge q du condensateur.
\(\phi\) est la phase à l'origine des dates (t=0).
A est l'amplitude maximale de la charge
\(\lambda\) est le coefficient d'amortissement
Les coefficients A, \(\lambda\) et \(\phi\) sont déterminés à partir des conditions initiales.
Régime critique -Régime apériodique⚓
Le régime critique est caractérisé par une résistance critique \(R_C\) qui sépare les évolutions du circuit RLC en régime pseudo-périodique ou en régime apériodique (sans oscillation). La résistance critique est obtenue à partir de l'équation caractéristique de l'équation différentielle en annulant le discriminant \(\Delta \).
\(\Delta' =\lambda^2-\omega_0^2=0\)
\(\lambda =\frac {R}{2L} =\omega_0 =\frac {1}{\sqrt {LC}}\)
d'où
\(R_C =2 \sqrt{\frac {L}{C}}\)
Exercice corrigé⚓
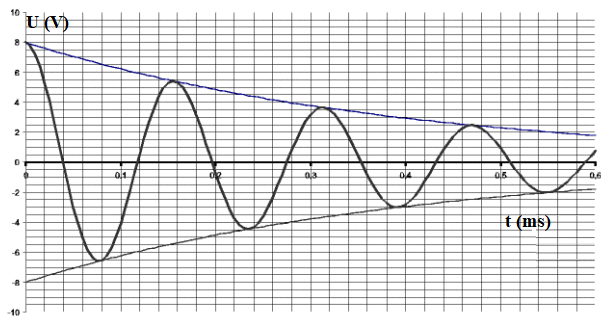
Le condensateur d'un circuit RLC série de capacité\( C=1\mu F\) est initialement chargé sous une tension de 10V.
A vous de jouer
Question⚓
La courbe ci-dessus est la tension aux bornes du condensateur.
Déterminer la pseudo-période.
Déduire de la question précédente la valeur de l'inductance L du circuit.
Expliquer l'allure de la courbe.